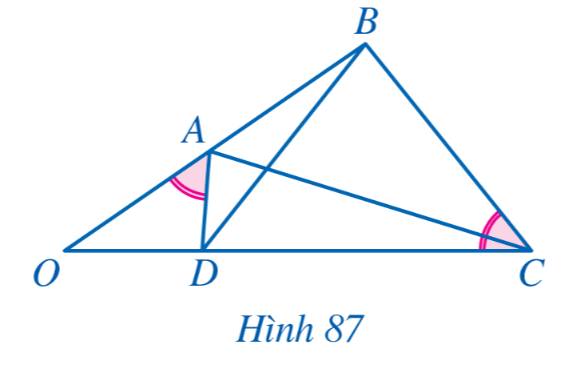
a) Xét tam giác OAD và tam giác OCB có:
\(\widehat {OAD} = \widehat {OCB};\,\,\widehat O\) chung
\( \Rightarrow \Delta OAD \backsim \Delta OCB\) (g-g)
b) Vì \(\Delta OAD \backsim \Delta OCB\) nên ta có \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\) (Tỉ số đồng dạng)
\( \Rightarrow \frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\)
c) Xét tam giác OAC và tam giác ODB có:
\(\frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\) và \(\widehat O\) chung
\( \Rightarrow \Delta OAC \backsim \Delta ODB\) (c-g-c)