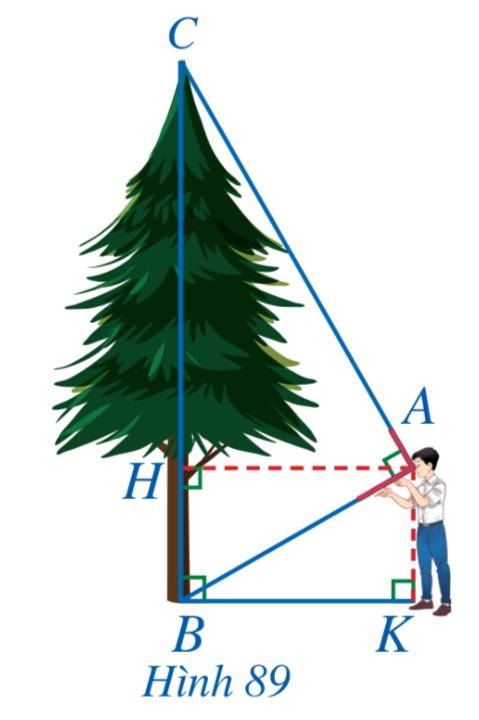
Xét tứ giác AHBK có \(\widehat H = \widehat B = \widehat K = 90^\circ \) nên AHBK là hình chữ nhật.
\( \Rightarrow AK = BH = 1,6m\)
Xét tam giác ABH vuông tại H có:
\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow 2,{8^2} + 1,{6^2} = A{B^2}\\ \Rightarrow A{B^2} = 10,4\\ \Rightarrow AB = \frac{{2\sqrt {65} }}{5}\end{array}\)
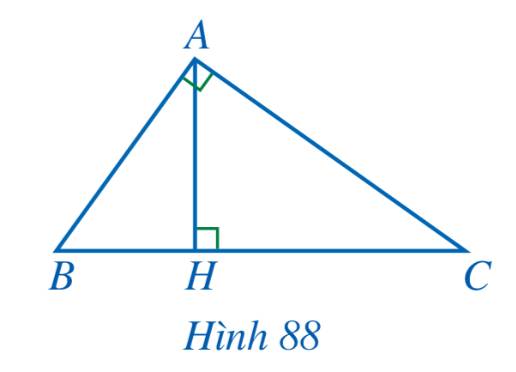
Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{BC}}{{BA}} = \frac{{AB}}{{HB}} \Leftrightarrow BC = A{B^2}:HB = {\left( {\frac{{2\sqrt {65} }}{5}} \right)^2}:1,6 = 6,5\)
Vậy cây cao 6,5m.