Chọn C
Ta có ![]()
![]()
![]()
![]()
![]() .
.
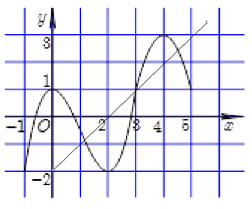
Dựa vào đồ thị ta thấy đường thẳng ![]() cắt đồ thị
cắt đồ thị ![]() tại hai điểm có hoành độ nguyên liên tiếp là
tại hai điểm có hoành độ nguyên liên tiếp là 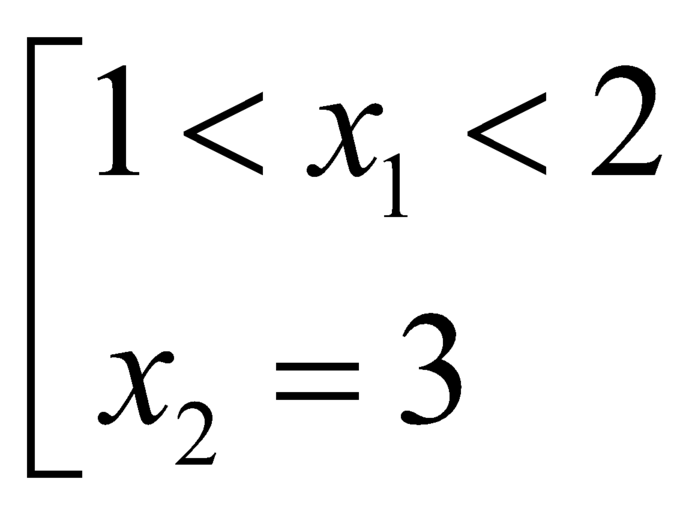 và cũng từ đồ thị ta thấy
và cũng từ đồ thị ta thấy ![]() trên miền
trên miền ![]() nên
nên ![]() trên miền
trên miền ![]()
![]() .
.
Vậy hàm số nghịch biến trên khoảng ![]() .
.
Chọn C

Ta có ![]()
![]()
![]()
![]()
![]() .
.
Dựa vào đồ thị ta thấy đường thẳng ![]() cắt đồ thị
cắt đồ thị ![]() tại hai điểm có hoành độ nguyên liên tiếp là
tại hai điểm có hoành độ nguyên liên tiếp là 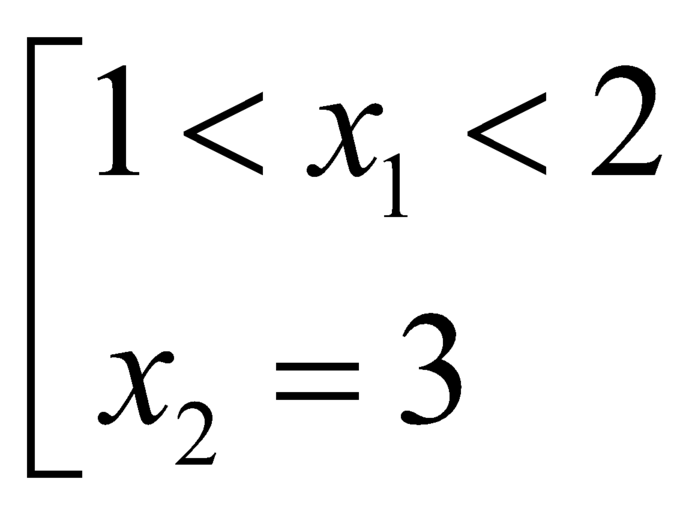 và cũng từ đồ thị ta thấy
và cũng từ đồ thị ta thấy ![]() trên miền
trên miền ![]() nên
nên ![]() trên miền
trên miền ![]()
![]() .
.
Vậy hàm số nghịch biến trên khoảng ![]() .
.
Cho hàm số y=f(x) có đồ thị của hàm số y=f'(x) được cho như hình bên. Hàm số
y
=
-
2
f
(
2
-
x
)
+
x
2
nghịch biến trên khoảng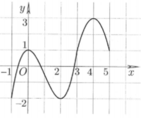
![]()
![]()
![]()
![]()
Cho hàm số y= f(x) có đạo hàm trên R thoả f( 2) = f( -2) =0 và đồ thị của hàm số y= f’ (x) có dạng như hình bên. Hàm số y= (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
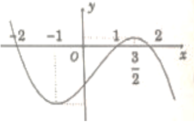
A. - 1 ; 3 2
B. (-1; 1)
C. (-2; -1)
D. (1; 2)
Cho hàm số y= f( x) có đạo hàm là hàm số y= f’(x) trên R. Biết rằng hàm số y= f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y= f( x) nghịch biến trên khoảng nào?
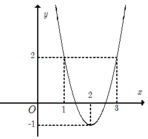
A. ![]() .
.
B. (- 1; 1)
C. ![]() .
.
D. ![]() .
.
Cho hàm số y= f(x) . Hàm số y= f ’( x) có đồ thị như hình bên. Hàm số ![]() nghịch biến trên khoảng?
nghịch biến trên khoảng?
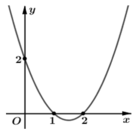
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) liên tục trên đoạn [1;4] và có đồ thị hàm số y=f'(x) như hình bên. Hỏi hàm số g(x)=f( x 2 + 2 ) nghịch biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
![]()
Cho hàm số f (x) Đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số g(x)=f(2-3x) nghịch biến trên khoảng nào trong các khoảng sau?

![]()
![]()
![]()
![]()
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
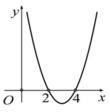
![]()
![]()
![]()
![]()
Cho hàm số y= f( x) có đạo hàm là hàm số f’(x) trên R. Biết rằng hàm số ![]() có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?
có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?

A. (-3; -1) và (1; 3).
B. (-1; 1) và (3; 5).
C. ![]() .
.
D. (- 5; -3) và (-1; 1).
Cho hàm số y= f(x). Hàm số y= f'(x) có đồ thị như hình bên. Hàm số y= f(2-x) đồng biến trên khoảng
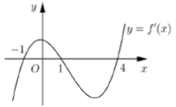
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.