Đáp án B

Vậy phương trình đã cho có 2 nghiệm thực phân biệt
Đáp án B



Vậy phương trình đã cho có 2 nghiệm thực phân biệt
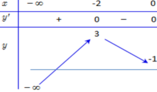
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ
Số nghiệm thực của phương trình 3f(x) +2 = 0 bằng
A. 1
B. 0
C. 3
D. 2
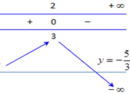
Cho hàm số f(x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 3f(x) -2 =0 là:
A. 1
B. 2
C. 3
D. 4
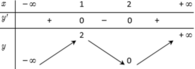
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
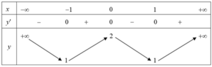
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - m =0 có 4 nghiệm phân biệt.
A. m ∈ ( 1 ; 2 ]
B. m ∈ [ 1 ; 2 )
C. m ∈ ( 1 ; 2 )
D. m ∈ [ 1 ; 2 ]
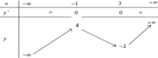
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tìm tất cả giá trị thực của tham số m để phương trình f(x) - m - 0 có bốn nghiệm phân biệt.
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có bảng biến thiên như sau:
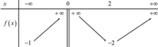
Tập hợp tất cả các giá trị thực của tham số m để phương trình f(x) + m = 0 có hai nghiệm phân biệt là
A. - ∞ ; 2
B. [ 1 ; 2 )
C. (1;2)
D. - 2 ; + ∞
Cho hàm số y=f(x) có bảng biến thiên như sau
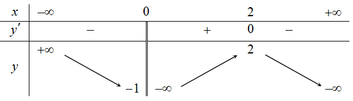
Tập hợp tất cả các giá trị thực của tham số m để phương trình f(x) + m = 0 có ba nghiệm phân biệt là
A. ![]() .
.
B. ![]() .
.
C. ![]()
D. ![]() .
.
Cho hàm số y=f(x) có bảng biến thiên như sau:
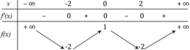
Tìm m để phương trình 2f(x+2019) - m = 0 có 4 nghiệm phân biệt.
A. m ∈ 0 ; 2
B. m ∈ - 2 ; 2
C. m ∈ - 4 ; 2
D. m ∈ - 2 ; 1
Cho hàm số y = f (x) có bảng biến thiên như sau
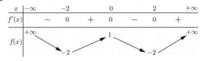
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số y=f(x) có bảng biến thiên dưới đây:

Để phương trình 3f(2x -1) = m-2 có 3 nghiệm phân biệt thuộc [0;1] thì giá trị của tham số m thuộc khoảng nào dưới đây?
A. - ∞ ; - 3
B. (1;6)
C. ( 6 ; + ∞ )
D. (-3;1)