Đáp án A.
Gọi M(x,y) là giao điểm của đồ thị (C) với trục tung.
Khi đó ta có x = 0 => y = -2.
Vậy M(0;-2)
Đáp án A.
Gọi M(x,y) là giao điểm của đồ thị (C) với trục tung.
Khi đó ta có x = 0 => y = -2.
Vậy M(0;-2)
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)
Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Tiếp tuyến của (C) tại giao điểm của (C) với trục tung có phương trình.
A. y = -3x + 1
B. y = -3x -2
C. y = 3x + 13
D. y = 3x - 2
Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
![]()
![]()
![]()
![]()
Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tìm tọa độ giao điểm M của đồ thị hàm số y = 2 x - 1 x + 2 và trục tung
A.![]()
B.![]()
C.![]()
D. ![]()
Đồ thị của hàm số f(x) = x 3 + 3 x 2 + b x + c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x = 1 tại điểm có tung độ bằng 3 khi
A. a = b = 0; c = 2
B. a = c = 0; b = 2
C. a = 2; b = c = 0
D. a = 2; b = 1; c = 0
Cho hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị (C) . Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là:
A. y = 8x + 1
B. y = 3x + 1
C. y = -8x + 1
D. y = 3x -1
Tọa độ giao điểm của đồ thị các hàm số:
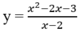
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).