Chọn B
y ' = x 2 - 2 x + ( m - 1 ) .
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = ( - 1 ) 2 - ( m - 1 ) = - m + 2 ≤ 0 ⇔ m > 2
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm điều kiện của m để hàm số y x3 - 3mx2 + 3(m + 2)x đồng biến trên R.
Đọc tiếp
Tìm điều kiện của m để hàm số y = x3 - 3mx2 + 3(m + 2)x đồng biến trên R.
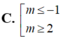
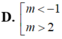
Tìm tất cả giá trị thực của tham số m để hàm số
y
x
3
3
+
(
m
+
1
)
x
2
+
(
3
m
+
1
)
x
+
2
đồng biến trên R A. B. C. D.
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để hàm số y = x 3 3 + ( m + 1 ) x 2 + ( 3 m + 1 ) x + 2 đồng biến trên R
A.
B.
C. 
D. 
20 tháng 6 2021 lúc 9:19
cho y=1/3x³-(m-2)x²+(m²-3m+2)x+3. tìm m để a)Hàm số đồng biến với mọi x thuộc (2;dương vô cùng) b)Hàm số đồng biến với mọi x thuộc (trừ âm vô cùng;0) c)Hàm số nghịch biến với mọi x thuộc (-2;3)
3 tháng 6 2021 lúc 16:08
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
2
(
m
-
1
)
x
2
+
(
m
-
1
)
x
+
5
đồng biến trên
ℝ
A.
m
∈
(
-
∞
;
1
]
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + 2 ( m - 1 ) x 2 + ( m - 1 ) x + 5 đồng biến trên ℝ
A. m ∈ ( - ∞ ; 1 ]
B. m ∈ 1 ; 7 4
C. m ∈ - ∞ ; 1 ∪ 7 4 ; + ∞
D. m ∈ 1 ; 7 4
tìm m để hàm số y = -x^3 + 3mx^2 - 2 luôn nghịc biến R
A. m = 0.
B. m > 0.
C. m ≠ 0.
D. M < 0.
Xác định giá trị của tham số m để hàm số
y
x
2
+
m
+
1
x
-
1
2
-
x...
Đọc tiếp
Xác định giá trị của tham số m để hàm số y = x 2 + m + 1 x - 1 2 - x
nghịch biến trên mỗi khoảng xác định của nó
A. m = −1; B. m > 1;
C. m ∈ (−1;1); D. m ≤ −5/2.
Tìm giá trị của tham số m để các hàm số y
x
3
- 2m
x
2
+ 12x - 7 đồng biến trên R.A. m 4 B. m
∈
(0;
∞
)C. m
∈
(-
∞
; 0) D. -3
≤
m
≤
3
Đọc tiếp
Tìm giá trị của tham số m để các hàm số y = x 3 - 2m x 2 + 12x - 7 đồng biến trên R.
A. m = 4 B. m ∈ (0; ∞ )
C. m ∈ (- ∞ ; 0) D. -3 ≤ m ≤ 3
Tìm giá trị của tham số m để các hàm số y = x 3 - 2m x 2 + 12x - 7 đồng biến trên R.
A. m = 4 B. m ∈ (0; ∞ )
C. m ∈ ( - ∞ ; 0) D. -3 ≤ m ≤ 3