Đáp án B
Ta có: 
; 
.
;
hàm số có hai điểm cực trị 
.
Mặt khác 
.
.
Hàm số bậc ba có đồ thị nhận điểm uốn làm tâm đối xứng. Do đó:
m cần tìm thoả và điểm uốn nằm trên trục hoành
=> m < 1 và 
.
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích S1= 8 3 và phần nằm phía dưới trục hoành có diện tích S2= 5 12 (tham khảo hình vẽ bên). Tính I = ∫ - 1 0 f ( 3 x + 1 ) d x .
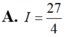
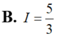
Cho hàm số y = 1 3 x 3 - x 2 + mx + m - 1 3 ( m là tham số thực). Tìm m để hình phẳng giới hạn bởi đồ thị hàm số và trục Ox được chia thành hai phần có diện tích bằng nhau.
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số y = x 4 - 6 x 2 + m có đồ thị C m .Giả sử C m cắt trục hoành tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi C m và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có diện tích bằng nhau. Khi đó m = a b (với a,b là các số nguyên, b > 0 ; a b là phân số tối giản). Giá trị của biểu thức S=a+b là:
A. 7.
B. 6.
C. 5.
D. 4.
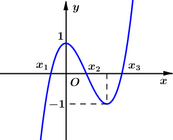
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng
A. 
.
B. 
.
C. 
.
D. 
.
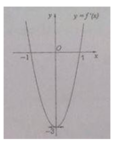
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị của hàm số Ox cho bởi hình vẽ dưới đây. Tính Thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giới hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox.
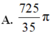
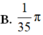
D. Đáp án khác
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 x 2 + 1 trục Ox và đường thẳng x=1 bằng a b - ln 1 + b c với a,b,c là các nguyên số dương. Khi đó giá trị của a+b+c là:
A. 11.
B. 12.
C. 13.
D. 14.
Tính thể tích hình tròng xoay khi quay quanh trục Ox một hình phẳng giới hạn bởi đồ thị hàm số y = 2 x + 1 x 2 + x + 1 trục Ox, hai đường thẳng x = 1 và x = 3.
A. π 13 13 - 3 3 3
B. π 26 13 + 6 3 3
C. π 26 13 - 6 3 3
D. π 2 13 13 + 3 3 3
.
.
.
.
