Với k ≥ 0 ta có:
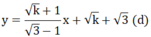
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
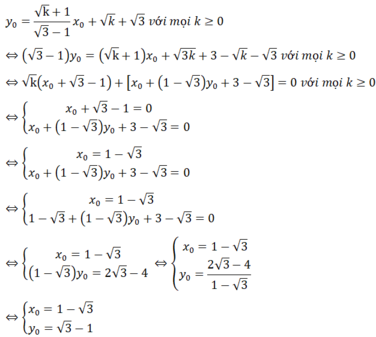
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ; 3 -1)
Với k ≥ 0 ta có:
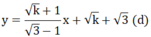
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
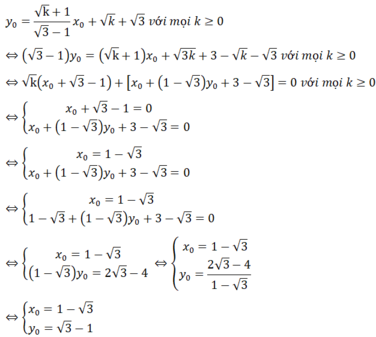
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ; 3 -1)
Cho hàm số y = k + 1 3 - 1 . x + k + 3 (d)
Chứng minh rằng, với mọi giá trị k ≥ 0, các đường thẳng (d) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm cố định đó.
chứng minh rằng
a) Họ đường thẳng k(x+3)-7-y=0 luôn đi qua điểm cố định với mọi k
b) Họ đường thẳng (m+2)x+(m-3)y-m+8=0 luôn đi qua điểm cố định với mọi m
c) Họ đường thẳng y=(2-k)x+k-5 luôn đi qua điểm cố định với mọi k
Cho đường thẳng (d): y= (m+1)x +2m -3. Chứng minh rằng với mọi m đường thẳng (d) luôn luôn đi qua một điểm cố định. Xác định điểm cố định đó.
Cho hàm số y = mx + (2m + 1) (1)
Với mỗi giá trị của m ∈ R, ta có một đường thẳng xác định bởi (1). Như vậy, ta có một họ đường thẳng các định bởi (1). Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm đó.
Cho hàm số y=mx+2m+1(d). Chứng minh rằng với mọi giá trị của m thì học đường thẳng d luôn đi qua 1 điểm cố định. Hãy xác định điểm cố định đó.
Chứng tỏ rằng đường thẳng mx + 3 + (3m - 1)y = 0 luôn đi qua một điểm cố định với mọi m. Tìm tọa độ điểm cố định đó?
Chứng minh rằng khi k thay đổi, các đường thẳng (k + 1)x – 2y = 1 luôn đi qua một điểm cố định. Tìm điểm cố định đó.
Chứng minh rằng khi k thay đổi, các đường thẳng (k + 1)x – 2y = 1 luôn đi qua một điểm cố định. Tìm điểm cố định đó.
Bài 1 : Cho 2 hàm số y= (2m-3)x+m-2 và y=(1-2m)x-m+3 có đồ thị là (d1) và (d2). Tìm m để (d2) cắt trục hoành tại điểm có hoành độ x=4.
Bài 2 : Cho đường thẳng (d) : y=(3k-5)x+k-1
a. tìm k để (d) và 2 đường thẳng y=-2x+3 ; y=x-6 đồng quy tại 1 điểm trên mặt phẳng tọa độ.
b. CM: đồ thị hàm số luôn đi qua 1 điểm cố định với mọi k. tìm điểm cố định ấy.