Đáp án A
Xét hàm số y = f(x) = x3 – 3x2 + m,![]()
f'(x) = 3x2 – 6x
Cho f’(x) = 0 <=> 3x2 – 6x = 0 <=>![]()
BBT
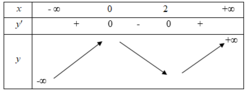
Suy ra hàm số đạt cực đại tại x = 0
Theo YCBT ta có f(0) = 2 ó m = 2
Đáp án A
Xét hàm số y = f(x) = x3 – 3x2 + m,![]()
f'(x) = 3x2 – 6x
Cho f’(x) = 0 <=> 3x2 – 6x = 0 <=>![]()
BBT

Suy ra hàm số đạt cực đại tại x = 0
Theo YCBT ta có f(0) = 2 ó m = 2
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
A. ![]()
B. 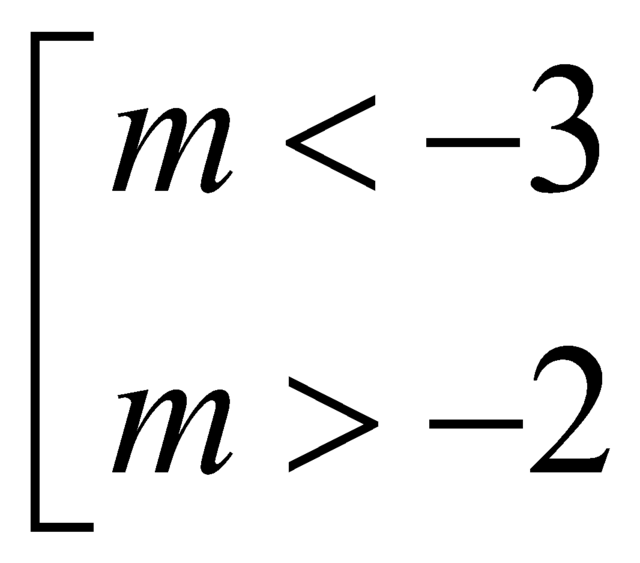
C. ![]()
D. ![]()
Tìm giá trị thực của tham số m để hàm số y = x 3 - 3 x 2 + m x đạt cực đại tại x =0
A. m=1.
B. m=2.
C. m=-2.
D. m=0.
Tìm giá trị thực của tham số m để hàm số y = x 3 - 3 x 2 + m x đạt cực đại tại x=0
A. 1
B. 2
C. -2
D. 0
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Cho hàm số y=x3+3x2+mx+m-2 với m là tham số thực, có đồ thị là (C) . Tìm tất cả các giá trị của m để (C) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
A. m<2
B. m ≤ 3
C. m<3
D. m ≤ 2 .