Chọn đáp án C
![]()
![]()
là đường thẳng cắt đồ thị tại 3 điểm phân biệt.
Do đó PT đã cho có 3 nghiệm phân biệt.
Chọn đáp án C
![]()
![]()
là đường thẳng cắt đồ thị tại 3 điểm phân biệt.
Do đó PT đã cho có 3 nghiệm phân biệt.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình
5f(x) +4 = 0
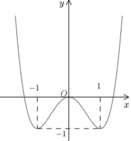
A. 4
B. 3
C. 2
D. 0
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Hàm số y= f'(x) có đồ thị như hình vẽ bên dưới:
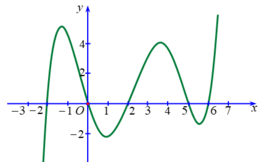
Số nghiệm thuộc đoạn [-2;6] của phương trình f(x) = f(0) là
A. 5
B. 2
C. 3
D. 4
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 2 f ( x 2 - 1 ) - 5 = 0 là:

A. 3
B. 2
C. 6
D. 4
Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
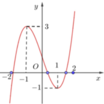
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x)) =0 bằng

A. 7
B. 3
C. 5
D. 9
Cho hàm số y=f(x) liên tục trên đoạn [-2;2], và có đồ thị là đường cong như trong hình vẽ bên. Hỏi phương trình f x - 1 = 2 - x có bao nhiêu nghiệm phân biệt trên đoạn [-2;2]
A. 2
B. 5
C. 4
D. 3
Cho hàm số f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
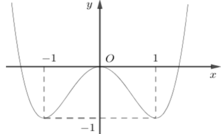
Số nghiệm của phương trình 4f(x) + 3 = 0 là:
A. 0
B. 2
C. 3
D. 4
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0; ln 3) là:
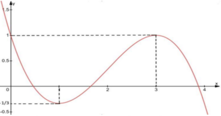
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên.
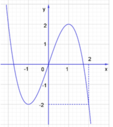
Số nghiệm của phương trình f(f(x)) = -2 là
A. 3.
B. 5.
C. 4.
D. 9.