Các câu hỏi tương tự
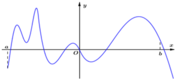
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên dưới. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau: I. Hàm số có 3 điểm cực trị. II. Hàm số g(x)đạt cực tiểu tại x0 III. Hàm số g(x) đạt cực đại tại x2 IV. Hàm số g(x) đồng biến trên khoảng (-2;0) V. Hàm số g(x) nghịch biến trên khoảng (-1;1) Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A.1 B.4 C.3 D.2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
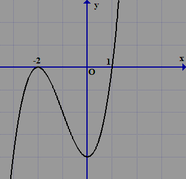
Cho hàm số y= f( x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới. Hàm số g(x) = 2f(x) + x2 đạt cực tiểu tại điểm
A . x=-1
B. x= 0
C . x= 1
D.x= 2
Cho hàm số
y
f
x
xác định và liên tục trên R, có đồ thị hàm số
y
f
x
như hình vẽ bên dưới. Hàm số
g
x
f
x
-...
Đọc tiếp
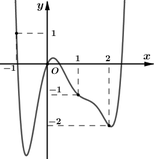
Cho hàm số y = f x xác định và liên tục trên R, có đồ thị hàm số y = f ' x như hình vẽ bên dưới. Hàm số g x = f x - 1 2 x 2 + x - 8 có bao nhiêu điểm cực tiểu?
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số y f(x) có đồ thị như hình vẽ bên dưới. Hàm số đã cho đạt cực tiểu tại điểm A. x -1 B. x1 C. x 0 D. x 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
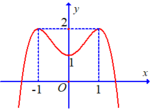
Hàm số đã cho đạt cực tiểu tại điểm
A. x= -1
B. x=1
C. x= 0
D. x= 2
Cho hàm số
y
f
x
có đạo hàm trên
ℝ
. Đồ thị hàm số như hình vẽ bên dưới. Số điểm cực tiểu của hàm số
g
x
2
f
x
+
2
+
x
+
1
x
+
3
là
Đọc tiếp
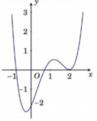
Cho hàm số y = f x có đạo hàm trên ℝ . Đồ thị hàm số như hình vẽ bên dưới.
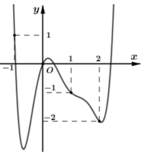
Số điểm cực tiểu của hàm số g x = 2 f x + 2 + x + 1 x + 3 là
![]()
![]()
![]()
![]()
Hàm số y f(x) có đạo hàm f’(x) trên khoảng . Hình vẽ bên là đồ thị của hàm số y- f’( x) trên khoảng . Hỏi hàm số y f(x) có bao nhiêu điểm cực trị? A . 0 B. 1 C. 3 D.4
Đọc tiếp
Hàm số y= f(x) có đạo hàm f’(x) trên khoảng ![]() . Hình vẽ bên là đồ thị của hàm số y=- f’( x) trên khoảng
. Hình vẽ bên là đồ thị của hàm số y=- f’( x) trên khoảng ![]() .
.
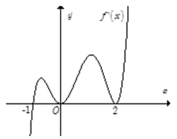
Hỏi hàm số y= f(x) có bao nhiêu điểm cực trị?
A . 0
B. 1
C. 3
D.4
Cho hàm số
y
a
x
4
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a...
Đọc tiếp
Cho hàm số y = a x 4 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a # 0 có đồ thị như hình vẽ bên.
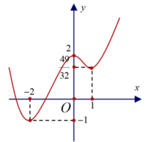
Các điểm cực tiểu của hàm số là
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y f’(x) . Hàm số y g(x) f(x) + x đạt cực tiểu tại điểm A. x 0 B.x 1 C. x 2 D. Không có điểm cực tiểu
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y= f’(x) . Hàm số y= g(x) = f(x) + x đạt cực tiểu tại điểm
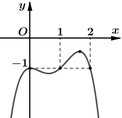
A. x= 0
B.x= 1
C. x= 2
D. Không có điểm cực tiểu
Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Hình vẽ bên là đồ thị của hàm số f'(x) trên khoảng K. Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
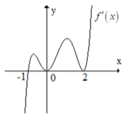
A. 0
B. 4
C. 3
D. 1