Chọn D.
Từ đồ thị ta suy ra các tính chất của hàm số:
1. Hàm số đạt CĐ tại x = 0 và đạt CT tại x = ± 1 .
2. Hàm số tăng trên - 1 ; 0 và 1 ; + ∞ .
3. Hàm số giảm trên - ∞ ; 0 và 0 ; 1 .
4. Hàm số không có tiệm cận.
Chọn D.
Từ đồ thị ta suy ra các tính chất của hàm số:
1. Hàm số đạt CĐ tại x = 0 và đạt CT tại x = ± 1 .
2. Hàm số tăng trên - 1 ; 0 và 1 ; + ∞ .
3. Hàm số giảm trên - ∞ ; 0 và 0 ; 1 .
4. Hàm số không có tiệm cận.
Cho hàm số y =f (x) có đồ thị (C) như hình vẽ. Chọn khẳng định sai về hàm số f (x):
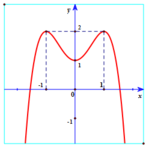
A. Hàm số f ( x ) có ba cực trị.
B. Hàm số f ( x ) có giá trị lớn nhất là 2 khi x = 1 .
C. Hàm số f ( x ) có giá trị nhỏ nhất là 1 khi x = 0 .
D. lim x → ± ∞ f ( x ) = - ∞ .
Cho hàm số y= f( x) có đồ thị hàm số y= f’(x) như hình vẽ
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A. ![]() .
.
B. (-2; 0)
C. (- 3; 1)
D . (1; 3)
Cho hàm số y= f( x) có đạo hàm là hàm số f’(x) trên R. Biết rằng hàm số ![]() có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?
có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?

A. (-3; -1) và (1; 3).
B. (-1; 1) và (3; 5).
C. ![]() .
.
D. (- 5; -3) và (-1; 1).
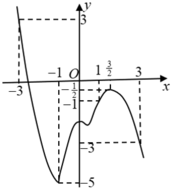
Cho hàm số y= f( x) có đạo hàm là hàm số y= f’(x) trên R. Biết rằng hàm số y= f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y= f( x) nghịch biến trên khoảng nào?
A. ![]() .
.
B. (- 1; 1)
C. ![]() .
.
D. ![]() .
.
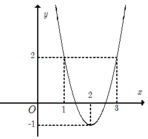
Hàm số f(x) có đạo hàm trên R là hàm số f’(x). Biết đồ thị hàm số f’(x)được cho như hình vẽ bên. Hàm số f(x) nghịch biến trên khoảng nào dưới đây?

A. − ∞ ; 0
B. 0 ; + ∞
C. − ∞ ; 1 3
D. 1 3 ; 1
Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

![]()
![]()
![]()
![]()
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
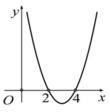
![]()
![]()
![]()
![]()
Cho hàm số y = f(x). Hàm số y = f’(x) có đồ thị như hình vẽ sau. Hàm số
y
=
f
(
2
-
e
x
)
đồng biến trên khoảng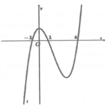
![]()
![]()
![]()
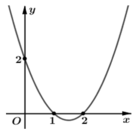
Cho hàm số y= f(x) . Hàm số y= f ’( x) có đồ thị như hình bên. Hàm số ![]() nghịch biến trên khoảng?
nghịch biến trên khoảng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.