Chọn B
Ta có: đường tiệm cận đứng của đồ thị hàm số là x = 1 = -c => c = -1.
Đường tiệm cận ngang của đồ thị hàm số là y = 1 = a => a = =1.
Đồ thị hàm số cắt trục hoành tại điểm 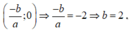 . Vậy a + 2b + 3c = 2.
. Vậy a + 2b + 3c = 2.
Chọn B
Ta có: đường tiệm cận đứng của đồ thị hàm số là x = 1 = -c => c = -1.
Đường tiệm cận ngang của đồ thị hàm số là y = 1 = a => a = =1.
Đồ thị hàm số cắt trục hoành tại điểm 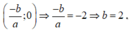 . Vậy a + 2b + 3c = 2.
. Vậy a + 2b + 3c = 2.
Cho hàm số y = a x + b x + c có đồ thị như hình bên dưới, với a,b,c ∈ ℤ . Tính giá trị của biểu thức T = a + 2b + 3c?
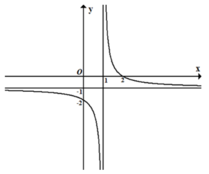
A. T = -8
B. T = 2
C. T = 6
D. T = 0
Cho hàm số y = ax + b x + c có đồ thị như hình vẽ bên dưới.
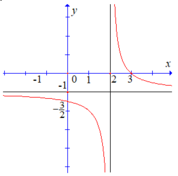
Giá trị của biểu thức a+2b+c bằng
A. -2
B. 0
C. 3
D. -1
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
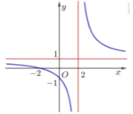
A. - 2
B. -3
C. - 4
D. -5
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hàm số y = a x - 1 b x + c có đồ thị như dưới đây. Tính giá trị biểu thức T = a + 2b + 3c
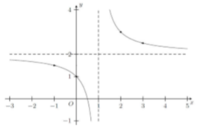
A. T = 1.
B. T = 2.
C. T = 3.
D. T = 4.
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
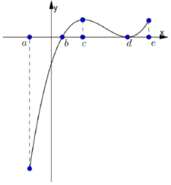
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ, đường thẳng d có phương trình y = x -1. Biết phương trình f(x)=0 có ba nghiệm x 1 < x 2 < x 3 . Giá trị của x 1 x 3 bằng
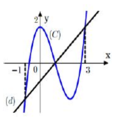
A. -2
B. - 5 2
C. 0
D. 1
Cho hàm số y=f(x) có đồ thị như hình vẽ và diện tích hai phần A, B lần lượt bằng 12 và 2. Giá trị của I = ∫ - 1 - 2 5 f ( 5 x + 3 ) d x bằng
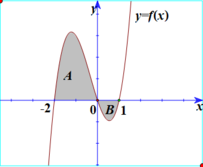
A. 50.
B. 14 5 .
C. 14.
D. 2 .
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m