áp án D
Phương pháp:
Nhận dạng hàm số bậc ba.
Cách giải:
Quan sát đồ thị hàm số, ta thấy: khi x → +∞ thì y → +∞ nên a > 0 ⇒ Loại các đáp án A, B, C. Chọn D.
Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là:
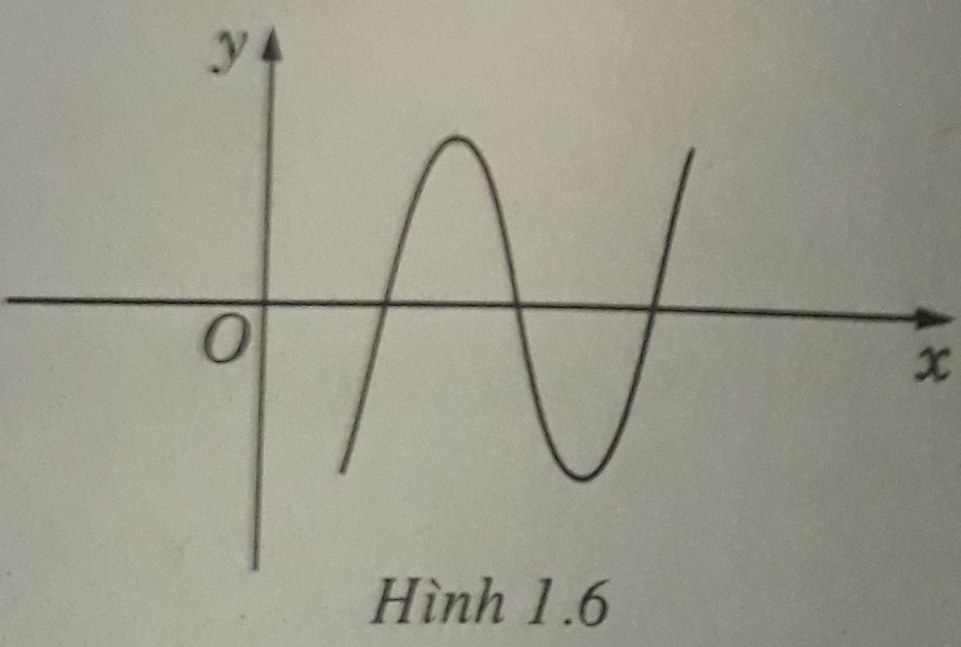
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3
Cho biết hàm số y=ax^3 + bx^2 + cx + dy=ax3+bx2+cx+d có đồ thị như hình trên. Trong các khẳng định sau, khẳng định nào đúng?
\A.{a>0b2−3ac=0
B{a>0b2−3ac<0
C,,{a<0b2−3ac>0
D,,{a<0b2−3ac=0
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:
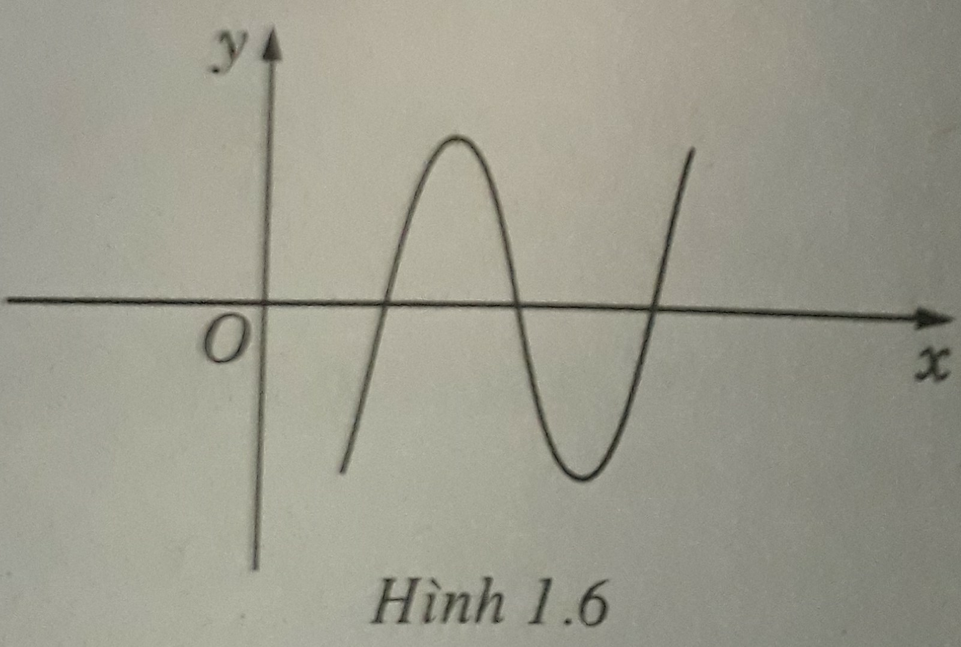
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3
Cho hàm số y = a x 4 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a # 0 có đồ thị như hình vẽ bên.
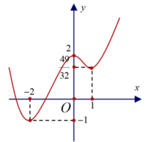
Các điểm cực tiểu của hàm số là
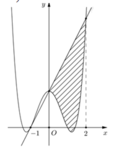
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
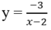
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có đồ thị như hình vẽ bên
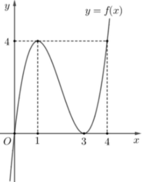
Phương trình f(f(f(f(x))) = 0 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 12
B. 40
C. 41
D. 16
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
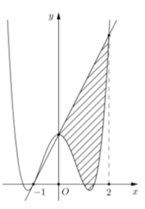
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Với giá trị nào của x thì đồ thị hàm số y = 2 / 3 x nằm phía trên đường thẳng y = 1?
A. x > 0 B. x < 0
C. x = 0 D. x < 1
