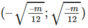Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔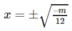 
Từ đó suy ra:
y’ > 0 với
y’ < 0 với
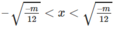
Vậy hàm số (1) đồng biến trên các khoảng
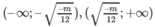
và nghịch biến trên khoảng
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu f'(x) như hình vẽ
Giá trị của tham số m để hàm số y = g ( x ) = f 1 - x + 1 x 2 + m x + m 2 + 1 chắc chắn luôn đồng biến trên (-3; 0)
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = 2 x 2 + 1 - m x + 1 + m x - m đồng biến trên 1 ; + ∞ là ( - ∞ ; a ] . Khi đó a thuộc khoảng nào ?
Cho hàm số y=f(x) có bảng biến thiên dưới đây:
Để phương trình 3f(2x -1) = m-2 có 3 nghiệm phân biệt thuộc [0;1] thì giá trị của tham số m thuộc khoảng nào dưới đây?
A. - ∞ ; - 3
B. (1;6)
C. ( 6 ; + ∞ )
D. (-3;1)
Trong tất cả các giá trị của tham số mm để hàm số y=\dfrac{1}{3} x^{3} +mx^{2} -mx-my=31x3+mx2−mx−m đồng biến trên \mathbb{R},R, giá trị nhỏ nhất của mm là
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau
Số giá trị nguyên của tham số m để hàm số y = f ( x 2 + 4 x + m ) nghịch biến trên - 1 ; 1 là
A. 1.
B. 3.
C. 2.
D. 0.
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng ( 1 ; + ∞ ) ?
A. 3.
B. 1.
C. 2.
D. 0.
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng 1 ; + ∞ ?
A. 3.
B. 1.
C. 2.
D. 0.
