Đáp án C
TXĐ:D = ℝ
y ' = 6 x 2 - 6 x + 5 > 0 ∀ x ∈ ℝ
suy ra hàm số đồng biến trên ℝ
ta có y ' ' = 12 x - 6 = 0 ⇒ = 1 2 . Vậy đồ thị hàm số nhận điểm I 1 2 ; - 4 là tâm đối xứngĐáp án C
Đáp án C
TXĐ:D = ℝ
y ' = 6 x 2 - 6 x + 5 > 0 ∀ x ∈ ℝ
suy ra hàm số đồng biến trên ℝ
ta có y ' ' = 12 x - 6 = 0 ⇒ = 1 2 . Vậy đồ thị hàm số nhận điểm I 1 2 ; - 4 là tâm đối xứngĐáp án C
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D=R\{3}.
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị.
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. 1,2,3.
B. 3,4.
C. 2,3,4.
D. 1,4.
Cho hàm số y = f x có đạo hàm trên ℝ . Đồ thị hàm số như hình vẽ bên dưới.
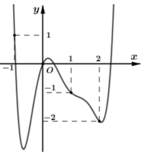
Số điểm cực tiểu của hàm số g x = 2 f x + 2 + x + 1 x + 3 là
![]()
![]()
![]()
![]()
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số y = a x 3 + b x 2 + c x + d . Biết rằng đồ thị hàm số có một điểm cực trị là M(1;-1) và nhận I(0;1) làm tâm đối xứng. Giá trị y(2) là:
A. y(2) = 2
B. y(2) = -2
C. y(2) = 6
D. y(2) = 3
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
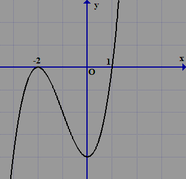
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
A. II,III,IV
B. I,II,III
C. III,IV
D. I,III,IV
Cho hàm số y=f(x) xác định và liên tục trên toàn trục số, hàm số f(x) có một điểm cực đại, một điểm cực tiểu với f C Đ = 3 ; f C T = 1 . Biết l i m x → - ∞ f ( x ) = - ∞ ; l i m x → + ∞ = + ∞ . Hỏi đồ thị (C) cắt trục hoành tại mấy điểm?
![]()
![]()
![]()
![]()
Cho hàm số y = f (x) có đạo hàm trên ℝ . Biết hàm số y = f ' x có đồ thị như hình vẽ. Hàm số g (x) = f (x) + x đạt cực tiểu tại điểm
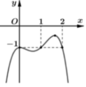
A. x = 1
B. x = 2
C.Không có điểm cực tiểu
D. x = 0
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị