Đáp án B
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là y = f'(x0).(x - x0) + y0
Cách giải:
![]()
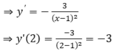
Vậy phương trình tiếp tuyến tại điểm M(2;5) là:
![]()
Đáp án B
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là y = f'(x0).(x - x0) + y0
Cách giải:
![]()
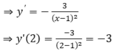
Vậy phương trình tiếp tuyến tại điểm M(2;5) là:
![]()
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
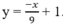
Cho hàm số:
y = 1 3 x 3 - m - 1 x 2 + m - 3 x + 4 1 2 (m là tham số) (1)
Viết phương trình của tiếp tuyến với đồ thị (C) tại điểm A(0; 9/2)
Tung độ giao điểm của hai đồ thị hàm số y = 3 x và y=11-x là
A.11
B. 3
C. 9
D. 2
Đồ thị (C) của hàm số y = 3 x + 1 x − 1 cắt trục tung tại điểm A. Tiếp tuyến của (C) tại A có phương trình là
A. y = -4x+1
B. y = -5x-1
C. y = 4x-1
D. y = 5x-1
Cho hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị (C) . Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là:
A. y = 8x + 1
B. y = 3x + 1
C. y = -8x + 1
D. y = 3x -1
Cho hàm số y = 1 3 x 3 - 2 x 2 + 3 x + 1 (C). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3 x - 1
A. y = 3 x + 1
B. y = 3 x - 29 3
C. y = 3 x + 20
D. Cả A và B đúng
Cho hàm số y =f(x); y = f(f(x)); y = f x 2 + 4 có đồ thị lần lượt là C 1 ; C 2 ; C 3 . Đường thẳng x = 1 cắt C 1 ; C 2 ; C 3 lần lượt tại M, N, P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y =3x + 2 và y = 12x - 5. Biết phương trình tiếp tuyến của C 3 tại P có dạng y = ax + b. Tìm a + b
A. 7.
B. 9
C. 8
D. 6
Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
![]()
![]()
![]()
![]()
Cho hàm số y = - x 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.