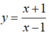Các câu hỏi tương tự
Cho hàm số y= (2x-1)/( x+1) có đồ thị (C). Gọi M là một điểm bất kì trên (C) . Tiếp tuyến của (C) tại M cắt các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận của (C). Tình diện tích của tam giác IAB
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C). Gọi M là một điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận của (C). Tính diện tích của tam giác IAB. A.2 B.12 C.4 D.6
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C). Gọi M là một điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận của (C). Tính diện tích của tam giác IAB.
A.2
B.12
C.4
D.6
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị C. Gọi M là một điểm bất kì trên C. Tiếp tuyến của C tại M cắt các đường tiệm cận của C tại A và B . Gọi I là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB. A. 2 B . 8 C. 6 D. 4
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị C. Gọi M là một điểm bất kì trên C. Tiếp tuyến của C tại M cắt các đường tiệm cận của C tại A và B . Gọi I là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB.
A. 2
B . 8
C. 6
D. 4
Cho hàm số có đồ thị (C): y
2
x
+
1
x
-
1
. Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ(với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là A. 2 B. 4 C. ...
Đọc tiếp
Cho hàm số có đồ thị (C): y = 2 x + 1 x - 1 . Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ(với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là
A. 2
B. 4
C. 2 3
D. 1
Cho hàm số
y
x
+
1
x
−
1
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai? A. M là trung điểm của AB B. Diện tích tam giác IAB là một số không đổi C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi D. Tổng khoảng...
Đọc tiếp
Cho hàm số y = x + 1 x − 1 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai?
A. M là trung điểm của AB
B. Diện tích tam giác IAB là một số không đổi
C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi
D. Tổng khoảng cách từ M đến hai tiệm cận là một số không đổi
Cho hàm số có đồ thị (C). Biết rằng tiếp tuyến tại một điểm M bất kỳ của (C) luôn cắt hai tiệm cận của (C) tại A và B. Độ dài ngắn nhất của đoạn thẳng AB là A.4B.
2
C.2D.2
2
B.
2
C.2 D.2
2
Đọc tiếp
Cho hàm số 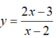 có đồ thị (C). Biết rằng tiếp tuyến tại một điểm M bất kỳ của (C) luôn cắt hai tiệm cận của (C) tại A và B. Độ dài ngắn nhất của đoạn thẳng AB là
có đồ thị (C). Biết rằng tiếp tuyến tại một điểm M bất kỳ của (C) luôn cắt hai tiệm cận của (C) tại A và B. Độ dài ngắn nhất của đoạn thẳng AB là
A.4B. 2 C.2D.2 2
B. 2
C.2
D.2 2
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến
∆
gần giá trị nào nhất? A. 6. B. 4. C. 3. D. 5.
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến ∆ gần giá trị nào nhất?
A. 6.
B. 4.
C. 3.
D. 5.
Cho hàm số y
2
x
-
1
x
-
1
có đồ thị (C). Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai tiệm cận của đồ thị (C) tại P và Q. Giá trị nhỏ nhất của đoạn thẳng PQ bằng A. 3
2
B. 4
2
C. 2
2
D.
2
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai tiệm cận của đồ thị (C) tại P và Q. Giá trị nhỏ nhất của đoạn thẳng PQ bằng
A. 3 2
B. 4 2
C. 2 2
D. 2
Cho hàm số
y
2
x
-
1
2
x
-
2
có đồ thị là (H). M là điểm thuộc (H) sao cho xM 1. Tiếp tuyến của (H) tại M cắt đường tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S∆OIB 8S∆OIA (trong đó O là gốc toạ độ, I là giao của hai tiệm cận). Hỏi có tất cả bao nhiêu điểm M. A. 2 B. 1 C. 3 D. Khôn...
Đọc tiếp
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị là (H). M là điểm thuộc (H) sao cho xM > 1. Tiếp tuyến của (H) tại M cắt đường tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S∆OIB = 8S∆OIA (trong đó O là gốc toạ độ, I là giao của hai tiệm cận). Hỏi có tất cả bao nhiêu điểm M.
A. 2
B. 1
C. 3
D. Không có M