Các câu hỏi tương tự
Cho đường tròn (O) và đường tròn (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài của cả 2 đường tròn (B, C là các tiếp điểm). tiếp tuyến chung trong của 2 đường tròn tại A cắt BC tại M a) CMR: A, , C thuộc đường tròn (M) đường kính BC b) Đường thẳng OO’ có vị trí như thế nào đối với đường tròn (M; BC/2) c) Xác định tâm của đường tròn đi qua O, M, O’ d) CMR: BC là tiếp tuyến của đường tròn đi qua O, M, O’.
Đọc tiếp
Cho đường tròn (O) và đường tròn (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài của cả 2 đường tròn (B, C là các tiếp điểm). tiếp tuyến chung trong của 2 đường tròn tại A cắt BC tại M a) CMR: A, , C thuộc đường tròn (M) đường kính BC b) Đường thẳng OO’ có vị trí như thế nào đối với đường tròn (M; BC/2) c) Xác định tâm của đường tròn đi qua O, M, O’ d) CMR: BC là tiếp tuyến của đường tròn đi qua O, M, O’.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ tiếp tuyến chung MN của (O) và (O') với M thuộc (O) và N thuộc (O') và A nằm trong tam giác BMN. Tiếp tuyến tại A của (O) cắt (O') tại C, MA cắt NC tại D
c/m MNDB nội tiếp
Cho hai đường tròn (O) và (O') cắt nhau tại A và B sao cho O và O' nằm khác phía với AB. Qua A kẻ cát tuyến cắt (O) và (O') lần lượt tại M và N. Tiếp tuyến của (O) tại M cắt tiếp tuyến của (O') tại N ở C. Xác định vị trí của cát tuyến MAN để bán kính đường tròn ngoại tiếp tam giác MCN đạt giá trị lớn nhất
CẦN GẤP Ạ!!! Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Các tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M. 1) Chứng minh bốn điểm M, B, O, A cùng thuộc một đường tròn và OA vuông góc BC 2) MC cắt đường tròn (O) tại D (D khác C) và tia BD cắt MA tại N. Chứng minh NA2 ND.NB và N trung điểm của AM 3) Kẻ đường kính AK của đường tròn (O), DK cắt BC tại E. Tính EC/BC.
Đọc tiếp
CẦN GẤP Ạ!!!
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Các tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M. 1) Chứng minh bốn điểm M, B, O, A cùng thuộc một đường tròn và OA vuông góc BC 2) MC cắt đường tròn (O) tại D (D khác C) và tia BD cắt MA tại N. Chứng minh NA2 = ND.NB và N trung điểm của AM 3) Kẻ đường kính AK của đường tròn (O), DK cắt BC tại E. Tính EC/BC.
Cho hai đường tròn ( O ) bán kính R và (O) bán kính R tiếp xúc ngoài với nhau tại M. Đường thằng OO cắt ( O) tại C, Cắt (O) tại D. Tiếp tuyến chung ngoài tiếp xúc với (O) tại A và (O) tại B, tiếp tuyến chung trong cắt AB tại I. Gọi B là giao điểm của BM và (O) , B khác Ma. Chứng minh AB2 4R.Rb. Chứng minh A , O , B thẳng hàngc. cho biết R 3R tính diện tích tứ giác MOIB theo R
Đọc tiếp
Cho hai đường tròn ( O ) bán kính R và (O') bán kính R' tiếp xúc ngoài với nhau tại M. Đường thằng OO' cắt ( O) tại C, Cắt (O') tại D. Tiếp tuyến chung ngoài tiếp xúc với (O) tại A và (O') tại B, tiếp tuyến chung trong cắt AB tại I. Gọi B' là giao điểm của BM và (O) , B' khác M
a. Chứng minh AB2 = 4R.R'
b. Chứng minh A , O , B thẳng hàng
c. cho biết R= 3R' tính diện tích tứ giác MOIB theo R
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O) cắt (O') tại C, của đường tròn (O') cắt (O) tại D. AB cắt CD tại M, N là trung điểm CD. Chứng minh góc CAM bằng góc DAN.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ tiếp tuyến chung MN của (O) và (O') với M thuộc (O) và N thuộc (O') và A nằm trong tam giác BMN. Tiếp tuyến tại A của (O) cắt (O') tại C, MA cắt NC tại D. CMR
a) góc NAD= góc ABD
b) ND tiếp xúc với đường tròn ngoại tiếp tam giác ABD
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ tiếp tuyến chung MN của (O) và (O') với M thuộc (O) và N thuộc (O') và A nằm trong tam giác BMN. Tiếp tuyến tại A của (O) cắt (O') tại C, MA cắt NC tại D. CMR
a) góc NAD= góc ABD
b)ND tiếp xúc với đường tròn ngoại tiếp tam giác ABD
Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)a, Chứng minh 4 điểm A,B,O,C thuộc một đường trònb. Trên cung nhỏ BC của (O) lấy điểm M ( M khác B, M khác C, M khác AO). Tiếp tuyến tại M cắt AB,AC lần lượt tại D và E. Chứng minh chu vi tam giác ADE2ABc, Đường thẳng vuông góc với AO tại O cắt AB và AC lần lượt tại P và Q. Chứng minh 4PO.QEPQ² Các a/chị ơi, e đang thắc mắc ở câu c ạ, hai câu a và b thì e đã có cách làm rồi ạ. Cảm ơn a/chị thậ...
Đọc tiếp
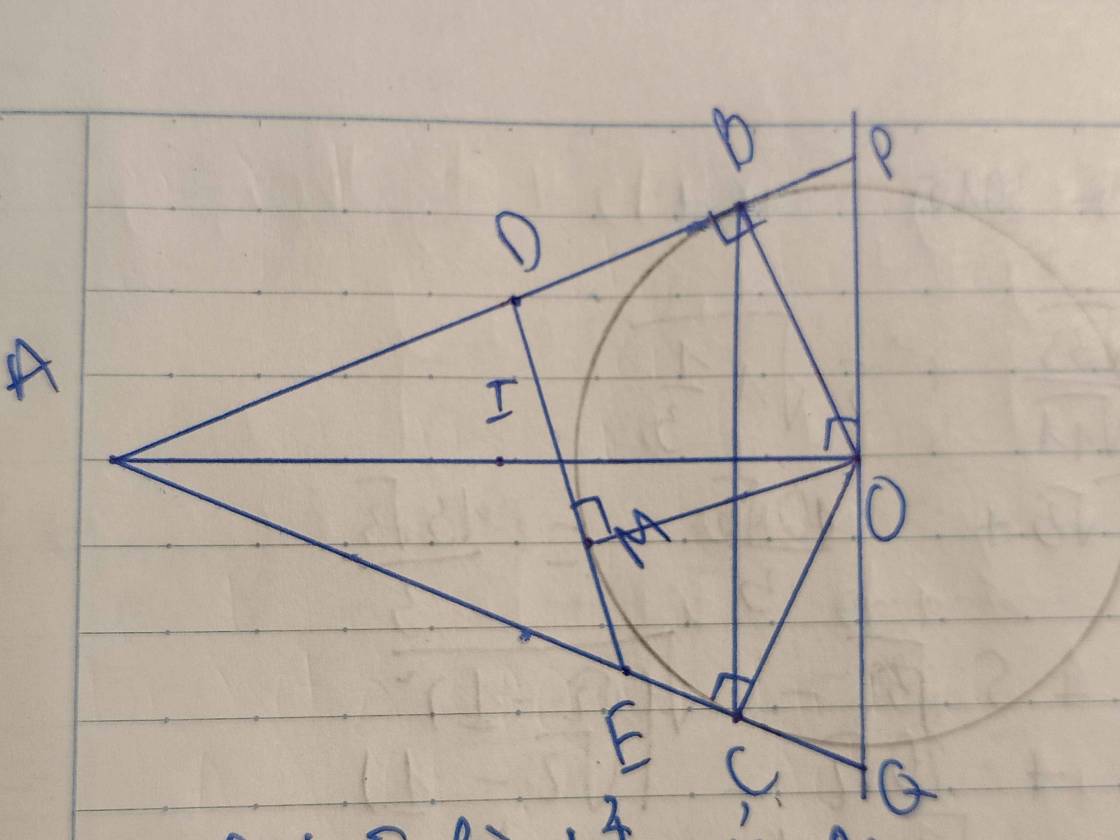Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)
a, Chứng minh 4 điểm A,B,O,C thuộc một đường tròn
b. Trên cung nhỏ BC của (O) lấy điểm M ( M khác B, M khác C, M khác AO). Tiếp tuyến tại M cắt AB,AC lần lượt tại D và E. Chứng minh chu vi tam giác ADE=2AB
c, Đường thẳng vuông góc với AO tại O cắt AB và AC lần lượt tại P và Q. Chứng minh 4PO.QE=PQ²
Các a/chị ơi, e đang thắc mắc ở câu c ạ, hai câu a và b thì e đã có cách làm rồi ạ. Cảm ơn a/chị thật nhiều ạ