Question

Cho hai tam giác vuông OAB và OCD như hình vẽ. Biết OB = OD = a, AB = OD = b. Tính cos A O C ^ theo a và b

A. 2 a b a 2 + b 2

B.  b 2 − a 2 a 2 + b 2

C. 1

D.  a 2 − b 2 a 2 + b 2

Answer 1

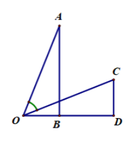
Xét ∆ OAB và  ∆ COD có:

  O B C ^ = C D O ^ = 90 0 (gt)

OB = CD (gt)

AB = OD (gt)

=>  ∆ OAB =  ∆ COD (c – g – c)

=> OA = OC (2 cạnh tương ứng)

=> OA.OC = O A 2 = O B 2 + A B 2 = a 2 + b 2 (Định lý Pytago)

cos A O C ^ = cos A O B ^ - C O D ^

= cos A O B ^ . cos C O D ^ + sin A O B ^ . sin C O D ^   

= O B O A . O D O C + A B O A . C D O C = O B . O D + A B . C D O A . O C  =  a b + a b a 2 + b 2 = 2 a b a 2 + b 2

Đáp án cần chọn là: A