Question

Cho hai tam giác ABC và MNP có \(AB = 2,BC = 5,CA = 6,MN = 4,NP = 10,PM = 12\).

Hãy viết các cặp góc tương ứng bằng nhau của hai tam giác trên và giải thích kết quả.

Answer 1

Ta thấy:

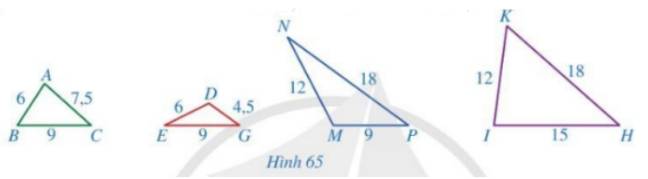
\(\begin{array}{l}\frac{{AB}}{{MN}} = \frac{2}{4} = \frac{1}{2}\\\frac{{BC}}{{NP}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{CA}}{{PM}} = \frac{6}{{12}} = \frac{1}{2}\\ \Rightarrow \frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}}\end{array}\)

Xét tam giác ABC và tam giác MNP có: \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}}\)

\( \Rightarrow \Delta ABC \backsim\Delta MNP\) (c-c-c)

\( \Rightarrow \widehat {ABC} = \widehat {MNP},\,\,\widehat {ACB} = \widehat {MPN},\,\,\widehat {BAC} = \widehat {NMP}\)