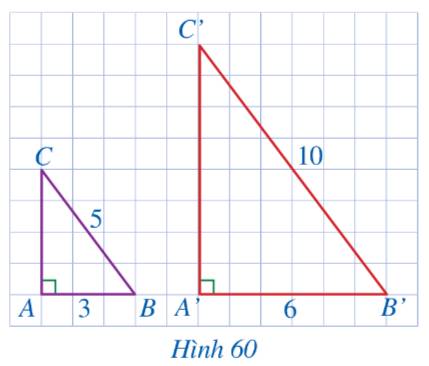
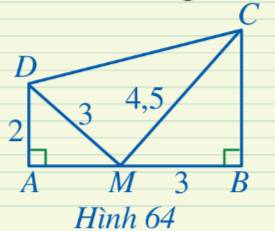
a) Xét tam giác ABC vuông tại A ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {3^2} + C{A^2} = {5^2}\\ \Leftrightarrow C{A^2} = {5^2} - {3^2}\\ \Leftrightarrow C{A^2} = 16\\ \Leftrightarrow CA = 4\end{array}\)
Xét tam giác A’B’C’ vuông tại A’ ta có:
\(A'B{'^2} + A'C{'^2} = B'C{'^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {6^2} + A'C{'^2} = {10^2}\\ \Leftrightarrow A'C{'^2} = {10^2} - {6^2}\\ \Leftrightarrow A'C{'^2} = 64\\ \Leftrightarrow A'C' = 8\end{array}\)
b) Ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{6}{3} = 2\\\frac{{B'C'}}{{BC}} = \frac{{10}}{5} = 2\\\frac{{C'A'}}{{CA}} = \frac{8}{4} = 2\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
c) Xét tam giác A’B’C’ và tam giác ABC có: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
\( \Rightarrow \Delta A'B'C' \backsim\Delta ABC\) (c-c-c)