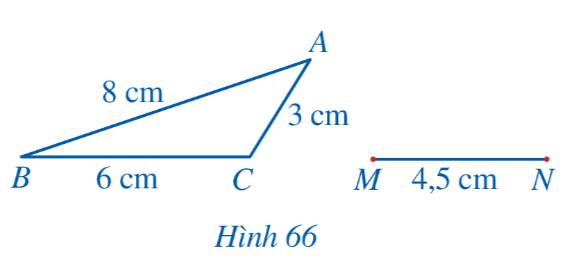
Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN với các kích thước như Hình 66. Bạn Hoa đố bạn Thanh vẽ điểm P thỏa mãn \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) mà không sử dụng thước đo góc. Em hãy giúp bạn Thanh sử dụng thước thẳng (có chia khoảng milimét) và compa để vẽ điểm P và giải thích kết quả tìm được.
Vì tổng ba góc trong một tam giác bằng \(180^\circ \) nên nếu \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) thì \(\widehat {MPN} = \widehat {CBA}\)
Ta cần \(\Delta ABC \backsim\Delta NPM\)
Khi đó \(\frac{{AB}}{{NP}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{NM}}\) hay \(\frac{8}{{NP}} = \frac{6}{{PM}} = \frac{3}{{4,5}} = \frac{2}{3}\)
Ta có: \(\frac{8}{{NP}} = \frac{2}{3} \Rightarrow NP = 8.3:2 = 12cm\)
\(\frac{6}{{MP}} = \frac{2}{3} \Rightarrow MP = 6.3:2 = 9cm\)
Vậy Thanh cần dùng thước kẻ vẽ hai đoạn thẳng NP=12cm và PM=9cm để tìm được điểm P thỏa mãn yêu cầu đề bài.