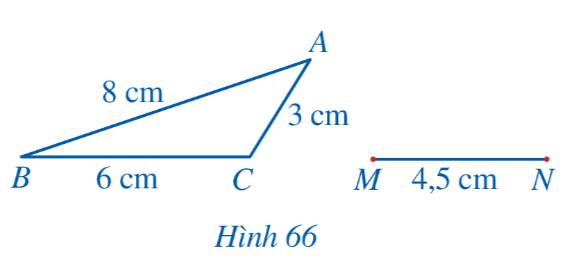
Bác Hùng vẽ bản đồ trong đó dùng ba đỉnh A, B, C của tam giác ABC lần lượt mô tả ba vị trí M, N, P trong thực tiễn. Bác Duy cũng vẽ một bản đồ, trong đó dùng ba đỉnh A', B', C' của tam giác A'B'C' lần lượt mô tả ba vị trí M, N, P đó. Tỉ lệ bản đồ mà bác Hùng và bác Duy vẽ lần lượt là 1 : 1 000 000 và 1 : 500 000. Chứng minh \(\Delta A'B'C'\; \backsim\Delta ABC\) và tính tỉ số đồng dạng.
Theo giả thiết, ta có:
\(\Delta ABC \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,000\,000}}\)
\(\Delta A'B'C' \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,500\,000}}\).
Từ đó ta có:
\(\begin{array}{l}\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}} = 1\,000\,000\\ \Rightarrow AB = 1\,000\,000MN,\,\,BC = 1\,000\,000NP,\,\,CA = 1\,000\,000PM\end{array}\)
và \(\begin{array}{l}\frac{{A'B'}}{{MN}} = \frac{{B'C'}}{{NP}} = \frac{{C'A'}}{{PM}} = 1\,500\,000\\ \Rightarrow A'B' = 1\,500\,000MN,\,\,B'C' = 1\,500\,000NP,\,\,C'A' = 1\,500\,000PM\end{array}\)
Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{1\,000\,000MN}}{{1\,500\,000MN}} = \frac{2}{3}\\\frac{{BC}}{{B'C'}} = \frac{{1\,000\,000NP}}{{1\,500\,000NP}} = \frac{2}{3}\\\frac{{CA}}{{C'A'}} = \frac{{1\,000\,000PM}}{{1\,500\,000PM}} = \frac{2}{3}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\end{array}\)
\( \Rightarrow \Delta ABC \backsim\Delta A'B'C'\) (c-c-c) với tỉ số đồng dạng là \(\frac{2}{3}\).