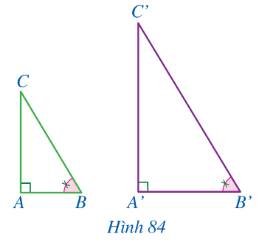
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\).

Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'BC\)
\( \Rightarrow \Delta ABC \backsim \Delta A'BC\)