Chọn D.
Từ giả thiết 1 < a < b ta có 0 < logaa < logab hay 1 < logab .
Áp dụng công thức đổi cơ số thì ![]() vì logba > 1 nên ta có: logba < 1 < logab.
vì logba > 1 nên ta có: logba < 1 < logab.
Chọn D.
Từ giả thiết 1 < a < b ta có 0 < logaa < logab hay 1 < logab .
Áp dụng công thức đổi cơ số thì ![]() vì logba > 1 nên ta có: logba < 1 < logab.
vì logba > 1 nên ta có: logba < 1 < logab.
Có bao nhiêu mệnh đề sau là đúng?
a > b > 0 ( a ≠ 1 ) ; log a b < 1
a > b > 1 ; log a b < log b a
1 > a > b > 0 ; log a b > 1
a > 1 > b > 0 ; log a b < 0
a > 1 > b > 0 ; log a b + log b a ≥ 2
A. 2
B. 3
C. 4
D. 5
Cho các số thực dương a, b với a ≠ 1 là log a b < 0 . Khẳng định nào sau đây đúng?
A. 0 < b < 1 < a 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < b < 1 < a 1 < a , b
D. 0 < b , a < 1 0 < a < 1 < b
Cho các số thực dương a, b với a ≠ 1 là log a b < 0 . Khẳng định nào sau đây đúng?
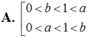
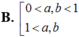
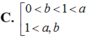
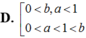
Cho các số thực dương a,b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
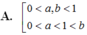
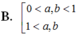
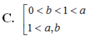
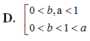
Cho các số thực dương a, b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
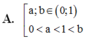
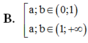
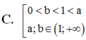
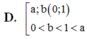
Cho các số thực dương a, b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b .
B. 0 < a , b < 1 1 < a , 1 < b .
C. 0 < b < 1 < a 1 < a , 1 < b .
D. 0 < b , a < 1 0 < a < 1 < b .
Cho các số thực dương a, b với a ≠ 0 và logab < 0. Khẳng định nào sau đây đúng?
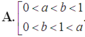
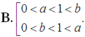
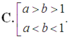
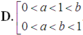
Cho 0 < a ≠ 1 , b > 0 thỏa mãn điều kiện log a b < 0 . Khẳng định nào sau đây là đúng
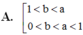
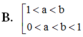
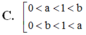
![]()
Kết quả rút gọn của biểu thức C = log a b + log b a + 2 log a b - log a b b log a b là:
A. logab
B. log a b
C. log a 2 b
D. log a b 3
Cho log a π < 0 ; log a b > 0 . Khẳng định nào sau đây là đúng?
A. a > 1 và b > 1
B. a > 1 và 0 < b < 1
C. 0 < a < 1 và b > 1
D. 0 < a < 1 và 0 < b < 1