Đáp án C.
Từ giả thiết, ta có 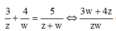
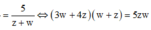
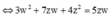
![]()
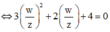
![]()
Lấy modun hai vế, ta được
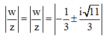
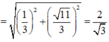
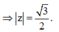
Đáp án C.
Từ giả thiết, ta có 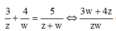
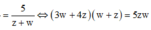
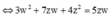
![]()
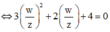
![]()
Lấy modun hai vế, ta được
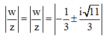
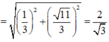
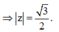
Cho số phức w = 1 + i 3 z + 2 , trong đó z là số phức thỏa mãn z - 1 ≤ 2 . Mệnh đề nào dưới đây đúng?
A. Tập hợp các điểm biểu diễn số phức w là hình tròn tâm 3 ; 3 , bán kính bằng 4.
B. Tập hợp các điểm biểu diễn số phức w là đường tròn tâm 3 ; - 3 , bán kính bằng 4.
C. Tập hợp các điểm biểu diễn số phức w là hình tròn tâm 3 ; 3 , bán kính bằng 2.
D. Tập hợp các điểm biểu diễn số phức w là đường tròn tâm 3 ; - 3 , bán kính bằng 2.
Cho hai số phức z và w khác 0 thoả mãn|z+3w|=5|w| và |z-2wi|=|z-2w-2wi| Phần thực của số phức z/w bằng
A.1.
B.-3.
C.-1.
D.3
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i
Cho số phức z = a + bi và w = 1 2 z + z ¯ . Mệnh đề sau đây là đúng?
A. w là một số thực
B . w = 2
C. wlà một số thuần ảo.
D. w = i
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 1 = 5 . Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = ( 2 + 3 i ) . z ¯ + 3 + 4 i là một đường tròn bán kính R. Tính R
A. R= 5 17
B. R= 5 10
C. R= 5 5
D. R= 5 13
Số phức z thỏa mãn z = 5 và số phức w = ( 1 + i ) z ¯ Tìm w
A. 10
B. 2 + 5
C. 5
D. 2 5
Cho số phức z thỏa mãn z - 1 = 5 Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = 2 + 3 i . z + 3 + 4 i là một đường tròn bán kính R. Tính R
![]()
![]()
![]()
![]()