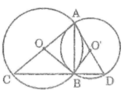
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90 °
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90 °
Ta có: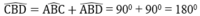
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD

Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90 °
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90 °
Ta có: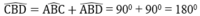
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.
Ví du 3. Cho hai đường tròn (O; R) và (O' R') cắt nhau tại A và B với R > R'. Vẽ
các đường kính AOC và AO'D. Chứng minh rằng ba điểm B, C, D thẳng hàng.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh ba điểm C, B, D thẳng hàng
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). Đường vuông góc với AO’ tại O’ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.
Cho hai đường tron tâm (O) và (O') cắt nhau tại A và B . Vẽ các đường kính AC và AD của hai đường tròn . Chứng minh ba điểm C, B, D thẳng hàng.
Cho tam giác ABC có ba góc nhọn ( AB bé hơn AC ) nội tiếp trong đường tròn tâm O. Hai đường cao BE và CF của tam giác ABC cắt nhau tại H.
a) chứng minh các tứ giác AEHF, BFEC nội tiếp được đường tròn
b) tia AH cắt BC tại D, kẻ đường kính AK của đường tròn tâm O. Chứng ming AB.AC= AD.2R
c) đường thẳng EF cắt đường tròn tâm O tại hai điểm M và N ( M thuộc cung nhỏ AB ). Chứng minh AM = AN
d) vẽ đường tròn tâm i đường kính AH cắt đường tròn tâm O tại S ( S khác A ), đường thẳng SA và BC cắt nhau tại T. Chứng minh ba điểm T, M, N thẳng hàng
Cho đường tròn (O;R) đường kính AB và dây CD vuông góc với nhau( CA<CB ).Hai tia BC và DA cắt nhau tại E. Từ E kẻ EH vuông góc với AB tại H; EH cắt CA tại F. CHứng minh rằng :
1.Tứ giác CDEF nội tiếp đường tròn.
2.Ba điểm B,D,F thẳng hàng
3.HC là tiếp tuyến của đường tròn O.
Cho hai đường tròn tâm O và O’ tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) ở B và cắt (O') ở C. Kẻ các đường kính BOD và CO'E của hai đường tròn trên
a, Chứng minh BD song song CE
b, Chứng minh ba điểm D, A, E thẳng hàng
c, Nếu (O) bằng (O') thì tứ giác BDCE là hình gì? Tại sao?