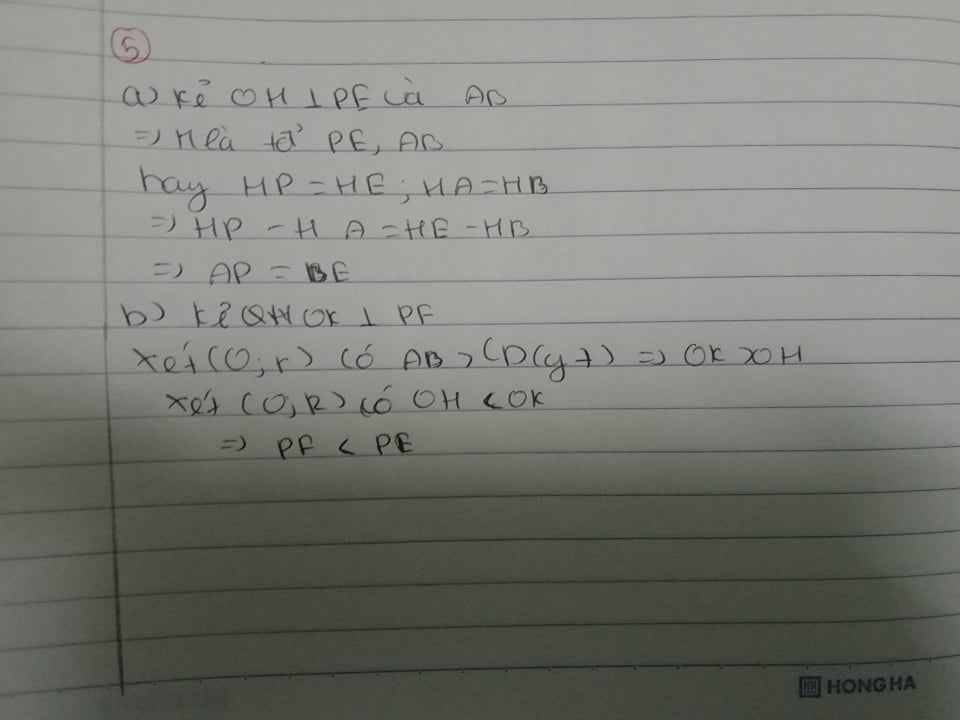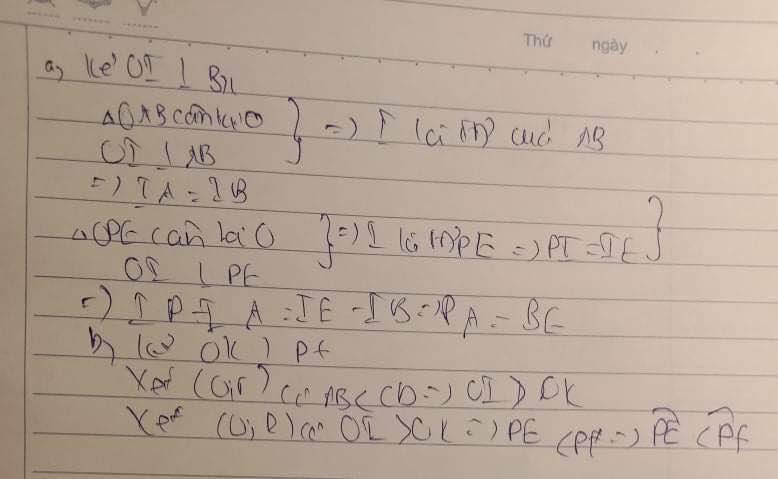Question

Cho hai đường tròn đồng tâm (O;R) và (O;r) với R > r. Từ một điểm P ở trên đường tròn (O ; R), kẻ hai tia Px, Py không qua O cắt hai đường tròn theo thứ tự ở A, B, E và C, D, F. Biết rằng AB > CD. Chứng minh rằng: 

a) PA = BE;

b) So sánh các cung nhỏ PE, PF.

Answer 1

a) Xét 2 TH:

- TH \(P_x,P_y\) nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)

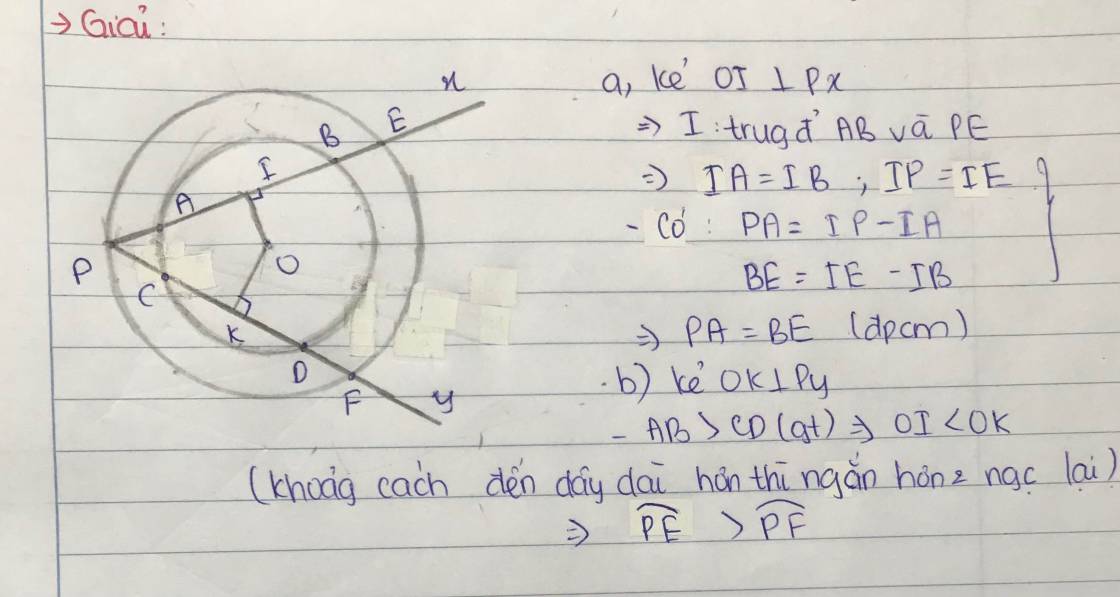
Kẻ \(OI\perp P_x\) ta có: 

\(IP=IE,IA=IB\)

\(\Rightarrow PI-AI=EI-BI\) hay PA=BE ( đpcm)

b) Kẻ \(OK\perp P_y\)

Trong đường tròn \(\left(O;r\right)\), vì AB>CD => OI<OK

Khi đó trong đường tròn \(\Rightarrow PE>PF\)

Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn \(\left(O;R\right)\)

ta có: cung PE > cung PF ( đpcm)

Answer 2

Giải :

a) kẻ OH vuông góc với PE bà AB

⇒ H là trđ PE, AB

hay HP = HE, HA = HB 

⇒ HP - HA = HE - HB

⇒ AP = BE.

b) kẻ OK vuông góc với PF

-Xét (O;r) có : AB > CD ( gt)

⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )

-Xét (O;R) có : OH < OK (cmt ) 

⇒ PE> PF.

     

Answer 3

a) CM ĐƯỢC IA = IB , IP=IE => PA=BE

b) VÌ AB> CD => OI<OK  => PE>PF => CUNG PE > CUNG PF

 

Answer 4

Answer 5

a,Kẻ BH vuông góc với AB và PE

=> H là trung điểm của AB và PE

hay HP=HE; HA=HB

=> HP-HA=HE-HP

=> AP=BE

b,kẻ OK vuông góc với PF

xét (O;r) có: AB> CD (GT)=> OK>OH

xét (O;R) có: OH< OK

=> PF< PE

Answer 6

a) Xét 2 TH:

- TH $P_x,P_y$ nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)

Kẻ $OI\perp P_x$ ta có: 

$IP=IE,IA=IB$

$\Rightarrow PI-AI=EI-BI$ hay PA=BE ( đpcm)

b) Kẻ $OK\perp P_y$

Trong đường tròn $\left(O;r\right)$, vì AB>CD => OI<OK

Khi đó trong đường tròn $\Rightarrow PE>PF$

Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn $\left(O;R\right)$

ta có: cung PE > cung PF ( đpcm)

Answer 7

a) kẻ OH vuông góc với PE bà AB

⇒ H là trđ PE, AB

hay HP = HE, HA = HB 

⇒ HP - HA = HE - HB

⇒ AP = BE.

b) kẻ OK vuông góc với PF

-Xét (O;r) có : AB > CD ( gt)

⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )

-Xét (O;R) có : OH < OK (cmt ) 

⇒ PE> PF

Answer 8

 

Answer 9

  

Answer 10

a)

Answer 11

Answer 12

Answer 13

a.Gọi OQ là đoạn thẳng vuông góc với PE tại Q

Vì OQ là đường kính vuông góc với AB nên Q là t/điểm của AB=>QA=QB

CMTT đường tròn (O;R):Q là trung điểm của PE=>QP=QE

Ta có:QA=QB;QP=QE

=>QP-QA=QB-QE

=>PA=PB

b.Vì AB>CD=>dây AB gần tâm (O) hơn dây CD

=>Dây PE gần tâm (O) hơn dây PF

=>PE>PF

Xét đường tròn (O;R) có:PE>PF

=>Cung nhỏ PE>cung nhỏ PF

Answer 14

a) Xét 2 TH:

- TH $P_x,P_y$ nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)

Kẻ $OI\perp P_x$ ta có: 

$IP=IE,IA=IB$

$\Rightarrow PI-AI=EI-BI$ hay PA=BE ( đpcm)

b) Kẻ $OK\perp P_y$

Trong đường tròn $\left(O;r\right)$, vì AB>CD => OI<OK

Khi đó trong đường tròn $\Rightarrow PE>PF$

Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn $\left(O;R\right)$

ta có: cung PE > cung PF ( đpcm)

Answer 15

  

Answer 16

 

 

Answer 17

a) kẻ OH vuông góc với PE bà AB

⇒ H là trđ PE, AB

hay HP = HE, HA = HB 

⇒ HP - HA = HE - HB

⇒ AP = BE.

b) kẻ OK vuông góc với PF

-Xét (O;r) có : AB > CD ( gt)

⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )

-Xét (O;R) có : OH < OK (cmt ) 

⇒ PE> PF.

Answer 18

a) kẻ OH vuông góc với PE bà AB

⇒ H là trđ PE, AB

hay HP = HE, HA = HB 

⇒ HP - HA = HE - HB

⇒ AP = BE.

b) kẻ OK vuông góc với PF

-Xét (O;r) có : AB > CD ( gt)

⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )

-Xét (O;R) có : OH < OK (cmt ) 

⇒ PE> PF.

Answer 19

Kẻ $OH\perp AB$ tại H và $OK\perp DE$ tại K.

Ta có: $AB<DE$ (gt)

$\Rightarrow OH>OK$ (định lí liên hệ giữa dây và khoảng cách đến tâm)

Trong đường tròn (O; R) có $OH>OK$

$\Rightarrow PC<PF$.do đó cung PC<cung PE

Answer 20

a) kẻ OH vuông góc với PE bà AB

⇒ H là trđ PE, AB

hay HP = HE, HA = HB

⇒ HP - HA = HE - HB

⇒ AP = BE.

b) kẻ OK vuông góc với PF

-Xét (O;r) có : AB > CD ( gt)

⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )

-Xét (O;R) có : OH < OK (cmt )

⇒ PE> PF. 
 

Answer 21

a) Xét 2 TH:

- TH ��,��Px​,Py​ nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)

Kẻ ��⊥��OI⊥Px​ ta có: 

$IP=IE,IA=IB$

$\Rightarrow PI-AI=EI-BI$ hay PA=BE ( đpcm)

b) Kẻ ��⊥��OK⊥Py​

Trong đường tròn $\left(O;r\right)$, vì AB>CD => OI<OK

Khi đó trong đường tròn $\Rightarrow PE>PF$

Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn $\left(O;R\right)$

ta có: cung PE > cung PF ( đpcm)