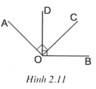
a) Ta có O C ⊥ O A nên A O C ^ = 90 ° ; O D ⊥ O B nên B O D ^ = 90 ° .
Tia OD nằm trong góc AOB nên A O D ^ + B O D ^ = A O B ^ .
⇒ A O D ^ = A O B ^ − B O D ^ = m ° − 90 ° (1)
Tia OC nằm trong góc AOB nên A O C ^ + B O C ^ = A O B ^
⇒ B O C ^ = A O B ^ − A O C ^ = m ° − 90 ° (2)
Từ (1) và (2), suy ra: A O D ^ = B O C ^ = m ° − 90 °
b) Tia OC nằm giữa hai tia OB và OD. Suy ra B O C ^ + D O C ^ = B O D ^ = 90 ° .
Nếu B O C ^ = D O C ^ thì D O C ^ = 90 ° : 2 = 45 ° .
Do đó A O D ^ = D O C ^ = C O D ^ ⇔ A O B ^ = 3. D O C ^ = 3.45 ° = 135 ° ⇔ m = 135 .
Chứng tỏ hai đường thẳng vuông góc