Question

Cho góc nhọn AOB. Trên nửa mặt phẳng bờ OA có chứa tia OB, vẽ tia O C ⊥ O A . Trên nửa mặt phẳng bờ OB có chứa tia OA vẽ tia O D ⊥ O B . Gọi OM và ON lần lượt là các tia phân giác của các góc AOD và BOC. Chứng tỏ rằng O M ⊥ O N .

Answer 1

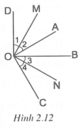
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .

Tia OB nằm giữa hai tia OA, OC.

Do đó A O B ^ + B O C ^ = 90 ° .  (1)

Tương tự, ta có A O B ^ + A O D ^ = 90 ° .        (2)

Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).

Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .

Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .

Vì   A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .

Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .

Do đó  M O N ^ = 90 ° ⇒ O M ⊥ O N