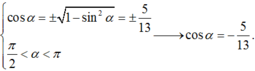Các câu hỏi tương tự
Cho góc α thỏa mãn
cos
α
-
12
13
và
π
2
α
π
.Tính tanα.
Đọc tiếp
Cho góc α thỏa mãn cos α = - 12 13 và π 2 < α < π .Tính tanα.
![]()
![]()
![]()
![]()
Cho góc α thỏa mãn
cos
α
-
5
3
v
à
π
α
3
π
2
. Tính tanα. A.
tan
α
-
3
5
B.
tan
α
2
5
C. ...
Đọc tiếp
Cho góc α thỏa mãn cos α = - 5 3 v à π < α < 3 π 2 . Tính tanα.
A. tan α = - 3 5
B. tan α = 2 5
C. tan α = - 4 5
D. tan α = - 2 5
Cho góc α thỏa mãn
cos
α
-
5
3
v
à
π
α
3
π
2
. Giá trị của tanα là : A.
tan
α
-
3
5
B.
tan
α
2
5...
Đọc tiếp
Cho góc α thỏa mãn cos α = - 5 3 v à π < α < 3 π 2 . Giá trị của tanα là :
A. tan α = - 3 5
B. tan α = 2 5
C. tan α = - 4 5
D. tan α = - 2 5
Cho góc α thỏa mãn
sin
α
3
5
v
à
π
2
α
π
.Tính
P
tan
α
1
+
tan
2
α
A.
P...
Đọc tiếp
Cho góc α thỏa mãn sin α = 3 5 v à π 2 < α < π .Tính P = tan α 1 + tan 2 α
A. P = 9 25
B. P = 3 25
C. P = 14 25
D. P = - 12 25
Cho góc α thỏa mãn
0
α
π
4
và
sin
α
+
cos
α
5
2
. Tính P sinα - cosα A.
P
3
2
B. P 1 C. P -1/2 D.
P
-...
Đọc tiếp
Cho góc α thỏa mãn 0 < α < π 4 và sin α + cos α = 5 2 . Tính P = sinα - cosα
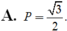 A.
P
=
3
2
A.
P
=
3
2
B. P = 1
C. P = -1/2
D. P = - 3 2
Cho góc α thỏa mãn
sin
π
+
α
-
1
3
v
à
π
2
α
π
Giá trị của
P
tan
7
π
2
-
α
là:...
Đọc tiếp
Cho góc α thỏa mãn sin π + α = - 1 3 v à π 2 < α < π
Giá trị của P = tan 7 π 2 - α là:
A. P = 2 2
B. P = - 2 2
C. P = 2 4
D. P = - 2 4
Cho cosα = 1/3, tính sin(α + π/6) - cos(α - 2π/3)
Cho góc α thỏa mãn
cos
α
-
5
3
và
π
α
3
π
2
.Tính tanα.
Đọc tiếp
Cho góc α thỏa mãn cos α = - 5 3 và π < α < 3 π 2 .Tính tanα.
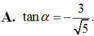
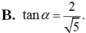
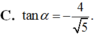
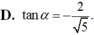
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z