Chọn D.
Ta có:
sin 2 α + cos 2 α = 1
sinα + 2cosα = -1 ⇔ sinα = -1 - 2cosα
⇔ (-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5 cos 2 α + 4cosα = 0
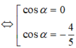
Vì π/2 < α < π ⇒ cosα < 0. Do đó, cos α = -4/5
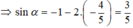
Ta lại có:
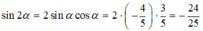
Chọn D.
Ta có:
sin 2 α + cos 2 α = 1
sinα + 2cosα = -1 ⇔ sinα = -1 - 2cosα
⇔ (-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5 cos 2 α + 4cosα = 0
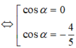
Vì π/2 < α < π ⇒ cosα < 0. Do đó, cos α = -4/5
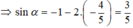
Ta lại có:
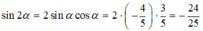
Cho góc α thỏa mãn π 2 < α < π và sinα + 2cosα = -1. Giá trị sin2α là:
A. 2 6 5
B. 24 25
C. - 2 6 5
D. - 24 25
Cho góc α thỏa mãn tanα = 2 và 180o < π < 270o. Giá trị của biểu thức P = cos α + sinα là:
A. P = - 3 5 5
B. P = 1 - 5
C. P = 3 5 2
D. P = 5 - 1 2
Cho góc α thỏa mãn sin π + α = - 1 3 v à π 2 < α < π
Giá trị của P = tan 7 π 2 - α là:
A. P = 2 2
B. P = - 2 2
C. P = 2 4
D. P = - 2 4
Cho góc α thỏa mãn cos α = - 5 3 v à π < α < 3 π 2 . Giá trị của tanα là :
A. tan α = - 3 5
B. tan α = 2 5
C. tan α = - 4 5
D. tan α = - 2 5
Cho sin2α = a với 0 < α < 90o. Giá trị của sinα + cosα bằng:
A. ( 2 - 1 ) a + 1
B. a + 1 - a 2 - a
C. ( 2 - 1 ) a + 1
D. a + 1
Cho góc α thỏa mãn sin α = 3 5 v à π 2 < α < π
Giá trị của biểu thức P = tan α 1 + tan 2 α là :
A. P = -3
B. P = 3 7
C. P = 12 25
D. P = - 12 25
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
Cho sinα = 0,6 với π 2 < α < π . Giá trị của cos2α bằng:
A. 0,96
B. -0,96
C. 0,28
D. -0,28
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π