Các câu hỏi tương tự
Cho hàm số y f(x) có bảng biến thiên như sau Bất phương trình
x
2
+
1
f
(
x
)
≥
m
có nghiệm trên khoảng (-1;2) khi và chỉ khi A. m10 B.
m
≤
15
C. m27 D. m15
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau
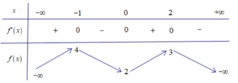
Bất phương trình x 2 + 1 f ( x ) ≥ m có nghiệm trên khoảng (-1;2) khi và chỉ khi
A. m<10
B. m ≤ 15
C. m<27
D. m<15
Cho hàm số f(x) liên tục trên có bảng biến thiên trên
-
1
;
2
như dưới đây. Tìm điều kiện m để phương trình có nghiệm
x
∈
-
1
;
2
.
Đọc tiếp
Cho hàm số f(x) liên tục trên có bảng biến thiên trên - 1 ; 2 như dưới đây. Tìm điều kiện m để phương trình có nghiệm x ∈ - 1 ; 2 .
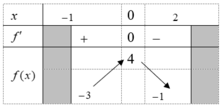
![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình dưới đây. (I). Hàm số nghịch biến trên khoảng (0;1). (II). Hàm số đồng biến trên khoảng (-1;2). (III). Hàm số có ba điểm cực trị. (IV). Hàm số có giá trị lớn nhất bằng 2. Số mệnh đề đúng trong các mệnh đề sau là: A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây.
(I). Hàm số nghịch biến trên khoảng (0;1).
(II). Hàm số đồng biến trên khoảng (-1;2).
(III). Hàm số có ba điểm cực trị.
(IV). Hàm số có giá trị lớn nhất bằng 2.
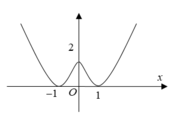
Số mệnh đề đúng trong các mệnh đề sau là:
A. 4
B. 2
C. 3
D. 1
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình dưới đây. (I). Hàm số nghịch biến trên khoảng (0;1). (II). Hàm số đồng biến trên khoảng (-1;2). (III). Hàm số có ba điểm cực trị. (IV). Hàm số có giá trị lớn nhất bằng 2 Số mệnh đề đúng trong các mệnh đề sau là: A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây.
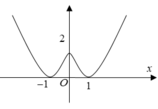
(I). Hàm số nghịch biến trên khoảng (0;1).
(II). Hàm số đồng biến trên khoảng (-1;2).
(III). Hàm số có ba điểm cực trị.
(IV). Hàm số có giá trị lớn nhất bằng 2
Số mệnh đề đúng trong các mệnh đề sau là:
A. 4
B. 2
C. 3
D. 1
Cho hàm số y f(x) có đạo hàm trên
ℝ
, thỏa mãn f(2) f(-2) 2019. Hàm số y f(x) có đồ thị như hình vẽ. Hỏi hàm số
g
x
f
x
-
2019
2
(1;2) nghịch biến trên khoảng nào dưới đây?
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f(2) = f(-2) = 2019. Hàm số y = f'(x) có đồ thị như hình vẽ. Hỏi hàm số g x = f x - 2019 2 (1;2) nghịch biến trên khoảng nào dưới đây?
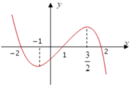
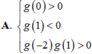
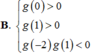
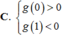
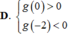
Cho hàm số y f(x) có đạo hàm trên
ℝ
, thỏa mãn f(2) f(-2) 2019. Hàm số y f(x) có đồ thị hàm số như hình vẽ. Hỏi hàm số g(x)
f
x
-
2019
2
(1;2). Ngịch biến trên khoảng nào dưới đây
A
.
1
;
2
B
.
-
2...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f(2) = f(-2) =2019. Hàm số y = f'(x) có đồ thị hàm số như hình vẽ. Hỏi hàm số g(x)= f x - 2019 2 (1;2). Ngịch biến trên khoảng nào dưới đây
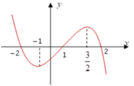
A . 1 ; 2
B . - 2 ; 2
C . 2 ; + ∞
D . - 2 ; - 1
Cho hàm số y f(x) có đạo hàm f(x). Hàm số y f(x) liên tục trên tập số thực và có bảng biến thiên như sau: Biết rằng f(-1)
10
3
, f(2) 6. Giá trị nhỏ nhất của hàm số g(x)
f
3
(
x
)
-
3
f
(
x
)
trên đoạn [-1;2] bằng A.
10
3
B.
820
27...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
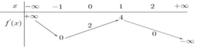
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Cho hàm số y f(x) có đồ thị . Khi đó f(x) nghịch biến trên các khoảng : A. , . B. , . C. , . D. , .
Đọc tiếp
Cho hàm số y = f(x) có đồ thị . Khi đó f(x) nghịch biến trên các khoảng :
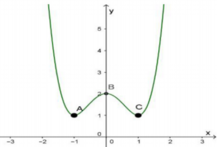
A. ![]() ,
, ![]() .
.
B. ![]() ,
,![]() .
.
C. ![]() ,
, ![]() .
.
D. ![]() ,
, ![]() .
.
Cho hàm số y f(x) nghịch biến trên
ℝ
và thỏa mãn [f(x) - x]f(x)
x
6
+
3
x
4
+
2
x
2
,
∀
x
∈
ℝ
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng A. 4 B. -28 C. -3 D. 33
Đọc tiếp
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33




