
Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.


Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
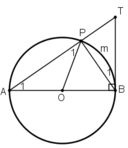
Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh
A P O ^ = P B T ^
cho đường tròn tâm O đường kính AB lấy điểm P khác A và B trên đường tròn .gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn .chứng minh góc APO=góc PBT
Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa đường tròn lấy điểm C (C khác A và B). Gọi D là giao điểm của đường thẳng BC với tiếp tuyến tại A của nửa đường tròn tâm O và I là trung điểm của AD a. Chứng minh BC.BD = 4R² b. Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O c. Từ C kẻ CH vuông góc với AB (H thuộc AB) BI cắt CH tại K. Chứng minh K là trung điểm của CH.
Cho nửa đường tròn tâm O,đường kính AB. Lấy M nằm trên đường tròn (M khác A và B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn tâm O lần lược tại C và D. Gọi CD giao AB tại P. Gọi E là giao điểm của AM và BD. F là giao điểm của AC và BM. Chứng minh E,F,P thẳng hàng
Cho đường tròn (O') đường kính AB .Lấy điểm P khác A và B trên đường tròn. G ọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn.Chứng minh góc APO = góc PBT
Cho đường tròn tâm O,đường kính AB.Lấy điểm P khác A trên đường tròn.Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh góc APO=góc PBT
Cho đường tròn tâm O có đường kính AB. Trên tiếp tuyến tại A của đường tròn (O), lấy điểm M khác điểm A. Vẽ tiếp tuyến thứ hai MC của đường tròn (O) (C là tiếp điểm). MB cắt đường tròn (O) tại D (D khác B). Gọi H là giao điểm của OM và AC.
a) Chứng minh góc ABH = góc CAD.
b) Gọi N là giao điểm của AC và BD. Chứng minh \(\frac{1}{MD}+\frac{1}{MB}=\frac{2}{MN}.\)
Cho đường tròn tâm O đường kính AC. Trên đường tròn (O) lấy điểm B (B khác A và C). Trên tia AB lấy điểm D sao cho AD=3AB. Đường thẳng vuông góc với DC tại D cắt tiếp tuyến Ax của (O) tại E. Gọi F là giao điểm thứ hai của DC với đường tròn (O), gọi H là giao điểm của BC và AF. Chứng minh rằng:
a) HB.HC=HA=HF
b) Tam giác BED cân
Cho nửa đường tròn (O) và đường kính AB=2R. Trên nửa đường tròn lấy C ( C khác A và B). Gọi D là giao điểm của đường thẳng BC với tiếp tuyến A của nửa đường tròn tâm O và I là trung điểm của AD.
Chứng minh BC.BD= 4R2Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O.Từ C kẻ CH vuộng góc với AB( H thuộc AB), BI cắt CH tại K. Chứng minh K là trung điểm của CH