c) Xét ΔOAC và ΔOBC có:
OA = OB = R
∠(AOC) = ∠(BOC) (tính chất đường chéo hình thoi)
OC là cạnh chung
⇒ ΔOAC = ΔOBC (c.g.c)
⇒ AC = BC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
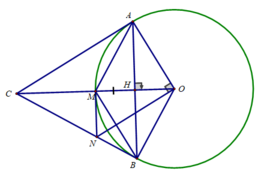
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
d) Đường thẳng vuông góc với OA tại O cắt BC tại N. Chứng minh MN là tiếp tuyến của đường tròn (O).
Cho đường tròn ( O : R ) ; M thuộc ( O ) . Đường trung trực của OM cắt đường tròn tại A và B ; cắt OM tại H
a. H là trung điểm AB và tam giác OAM đều
b. OAMB là hình thoi c. vẽ tiếp tuyến tịa A cắt OM tại C . chứng minh CA=CB
c. vẽ tiếp tuyến tịa A cắt OM tại C . chứng minh CA=CB
Ahuhu, 4h chiều phải nộp rồi. Bợn nào giúp Phương chime giùm.......................
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
b) Chứng minh tứ giác OAMB là hình thoi.
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
a) Chứng minh H là trung điểm của AB và tam giác OMA đều.
Cho điểm M thuộc đường trong (O) , bán kính R, đường trung trực của đoạn OM cắt đường tròn O tại điểm A và B cắt OM tại Ha) Chứng minh H là trung điểm của AB , tam giác AOM đềub) Vẽ tiếp tuyến tại A,B cắt nhau tại C .CM : O;M;C thẳng hàng .Tính AC , AH theo Rc) Đường thẳng vuông góc với OA tại O cắt BC tại N . CMinh : MN là tiếp tuyếncủa đường tròn (O) và M là tâm đường tròn nội tiếp tam giác ABC
Đọc tiếp
Cho điểm M thuộc đường trong (O) , bán kính R, đường trung trực của đoạn OM cắt đường tròn O tại điểm A và B cắt OM tại H
a) Chứng minh H là trung điểm của AB , tam giác AOM đều
b) Vẽ tiếp tuyến tại A,B cắt nhau tại C .CM : O;M;C thẳng hàng .
Tính AC , AH theo R
c) Đường thẳng vuông góc với OA tại O cắt BC tại N . CMinh : MN là tiếp tuyếncủa đường tròn (O) và M là tâm đường tròn nội tiếp tam giác ABC
cho đường tròn tâm O bán kính R 2 tiếp tuyến tại A và B của đường tròn cắt nhau tại điểm M đoạn thẳng OM cắt đường tròn (O) tại điểm I , cắt AB tại điểm K a)chứng minh 4 điểm M,A,O,B cùng thuộc đường tròn b)chứng minh OM.OK=R^2 và điểm I là tâm đường tròn nội tiếp tam giác MAB
Cho hai đường tròn đồng tâm (O;R) và (O; ). Trên đường tròn nhỏ lấy một điểm M . Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B. Tia OM cắt đường tròn lớn tại C. a) Chứng minh rằng = ( cung CA bằng cung CB) b) Tính số đo của hai cung AB
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
Đọc tiếp
Câu 4:( 4 điểm ) Từ điểm M nằm ngoài đường tròn ( O,R ) sao cho OM = 3R, vẽ các tiếp tuyến MA, MB với đường tròn ( O,R ) (A, B là các tiếp điểm). a ) Chứng minh: Tứ giác MAOB nội tiếp và OM là đường trung trực của đoạn AB. b ) Tính độ dài đoạn thẳng MA, AB theo R. c) Vẽ dây AC song song MB, đường thẳng MC cắt đường tròn (O,R) tại điểm thứ hai là D, tia AD cắt MB tại E. Chứng minh: E là trung điểm của đoạn MB
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.