Các câu hỏi tương tự
Cho đường tròn tâm O có hai đường kính AB và CD vuông góc với nhau. Lấy M cung nhỏ AC, vẽ tiếp tuyến với đường tròn tâm O tại M cắt đường thẳng CD tại S. CM góc MSD = 2lần góc MBA
cho đường tròn tâm O và 2 đường kính AB, CD vuông góc với nhau. Lấy 1 điểm M trên cung AC. Vẽ tiếp tuyến với đường tròn O tại N. Tiếp tuyến này cắt đường thẳng CD tại K. CMR : góc MKD = 2 góc MBA
Cho đường tròn tâm O có hai đường kính là AB và CD vuông góc với nhau tại O. Trên cung nhỏ BC lấy điểm M, AM cắt CD tại I. Tiếp tuyến của O tại M cắt tia AB tại N. Chứng minh rằng: AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CMI.
Cho đường tròn (O;R) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy điểm M thuộc cung nhỏ BC,AM cắt CD tại E. Qua kẻ tiếp tuyến với đường tròn (O) cắt đường thẳng BM tại N . Chứng minh bốn điểm M,N,D,E cùng nằm trên một đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.a. Chứng minh OA vuông góc với BC tại H.b. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn(O) tại E (E khác D). Chứng minh: AE.AD AC^2c. Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh rằng FD là tiếp tuyến của đường tròn (O).
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn này. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a. Chứng minh OA vuông góc với BC tại H.
b. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn(O) tại E (E khác D). Chứng minh: AE.AD = AC^2
c. Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh rằng FD là tiếp tuyến của đường tròn (O).
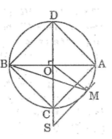
Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Bài3 : Cho đường tròn (O) , đường kính AB6cm . Trên đoạn OB lấy điểm M sao cho MB 1cm . Qua M vẽ dây CD của đường tròn (O) vuông góc với AB .a) Chứng minh: △ABC vuông . Tính CB , CDb) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn O ở Ec) Gọi F là giao điểm của AC và DB . Kẻ FH ⊥ AB tại H . Gọi K là giao điểm của CB và FH d) Chứng minh : Ba điểm H, C, E thẳng hàng .giải cụ thể chi tiết giúp mk vớiiiiiii ạ
Đọc tiếp
Bài3 : Cho đường tròn (O) , đường kính AB=6cm . Trên đoạn OB lấy điểm M sao cho MB = 1cm . Qua M vẽ dây CD của đường tròn (O) vuông góc với AB .
a) Chứng minh: △ABC vuông . Tính CB , CD
b) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn O ở E
c) Gọi F là giao điểm của AC và DB . Kẻ FH ⊥ AB tại H . Gọi K là giao điểm của CB và FH
d) Chứng minh : Ba điểm H, C, E thẳng hàng .
giải cụ thể chi tiết giúp mk vớiiiiiii ạ
GIẢI GIÚP HA MIK NHA MỌI NGƯỜI 2) CHO ĐƯỜNG TRÒN (O) VÀ ĐIỂM M NẰM NGOÀI ĐƯỜNG TRÒN. VẼ 2 TIẾP TUYẾN MA,MB VỚI(O),(A,B LÀ TIẾP ĐIỂM).VẼ ĐƯỜNG KÍNH BC CỦA (O) VÀ GỌI H LÀ HÌNH CHIẾU CỦA A TRÊN ĐƯỜNG KÍNH BC CỦA(O).CHỨNG MINH MC ĐI QUA TRUG ĐIỂM I CỦA AH.3) CHO NỬA ĐƯỜNG TRÒN (O) ĐƯỜNG KÍNH AB2R VÀ LẤY ĐIỂM H TRÊN CẠNH OB QU H VẼ DÂY CD VUÔNG GÓC VỚI AB. TIẾP TUYẾN C CẮT CÁC TIẾP TUYẾN TẠI A,B CỦA(O) TẠI M,N; BM CẮT` CD TẠI I. CHỨNG MINH A,N,I THẲNG HÀNG.
Đọc tiếp
GIẢI GIÚP HA MIK NHA MỌI NGƯỜI
2) CHO ĐƯỜNG TRÒN (O) VÀ ĐIỂM M NẰM NGOÀI ĐƯỜNG TRÒN. VẼ 2 TIẾP TUYẾN MA,MB VỚI(O),(A,B LÀ TIẾP ĐIỂM).VẼ ĐƯỜNG KÍNH BC CỦA (O) VÀ GỌI H LÀ HÌNH CHIẾU CỦA A TRÊN ĐƯỜNG KÍNH BC CỦA(O).CHỨNG MINH MC ĐI QUA TRUG ĐIỂM I CỦA AH.
3) CHO NỬA ĐƯỜNG TRÒN (O) ĐƯỜNG KÍNH AB=2R VÀ LẤY ĐIỂM H TRÊN CẠNH OB QU H VẼ DÂY CD VUÔNG GÓC VỚI AB. TIẾP TUYẾN C CẮT CÁC TIẾP TUYẾN TẠI A,B CỦA(O) TẠI M,N; BM CẮT` CD TẠI I. CHỨNG MINH A,N,I THẲNG HÀNG.