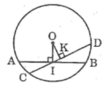
Gọi CD là dây bất kì đi qua I và CD không vuông góc với OI.
Kẻ OK ⊥ CD
Tam giác OKI vuông tại K nên OI > OK
Suy ra : AB < CD (dây lớn hơn gần tâm hơn)
Vậy dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.

Gọi CD là dây bất kì đi qua I và CD không vuông góc với OI.
Kẻ OK ⊥ CD
Tam giác OKI vuông tại K nên OI > OK
Suy ra : AB < CD (dây lớn hơn gần tâm hơn)
Vậy dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.
Bài 1: Cho một đường tròn (O) dây AB = 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.
Bài 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA = PB.
Bài 3: Cho đường tròn (O;5) và một dây cung AV dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M. Tính độ dài dây cung MA.
Bài 4: Cho đường tròn (O) và một điểm P bên trong đường tròn. Cmr trong tất cả dây đi qua P thì dây vuông góc với OP tại P là dây cung ngắn nhất.
Cho đường tròn (O), điểm I nằm bên trong đường tròn (I khác O). Dựng dây AB đi qua I và có độ dài ngắn nhất.
cho đường tròn(O) và điểm I nằm bên trong dường tròn a/chứng minh rằng dây Ab vuông góc với OI tai diểm I b/cho bán kính đường tròn bằng 5cm,khoảng cách từ tâm O đến AB là 3cm.Tính độ dài dây AB
Mn giải giúp mk bài này vs ạ
Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng: OI là tia phân giác của một trong hai góc tạo bởi hai dây AB, CD.
Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. Hãy cho biết ACBD là hình gì? Vì sao?
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.
Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng: Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một.
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.