Question

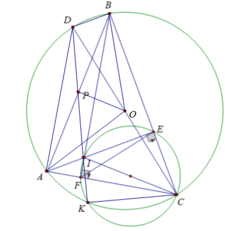
Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.

d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.

Answer 1

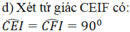
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF

Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)

DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)

⇒ D; I; K thẳng hàng (1)

Ta có:

DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)

AI ⊥ BC ( AI là đường cao của tam giác ABC)

⇒ AI // BD

DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)

BI ⊥ BA ( BI là đường cao của tam giác ABC)

⇒ AD // BI

Xét tứ giác ADBI có: AI // BD và AD // BI

⇒ ADBI là hình bình hành

Do P là trung điểm của AB ⇒ P là trung điểm của DI

Hay D; P; I thẳng hàng (2)

Từ (1) và (2) ⇒ D; P; K thẳng hàng.