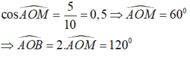
Đáp án A
Ta có: OA = OB = R nên tam giác ABO là cân tại O (1)
Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là tia phân giác của góc AOB (2)
Từ (1) và (2) suy ra: OH là đường cao trong tam giác AOB hay OH ⊥ Ab.
* Xét tam giác vuông AOM có :
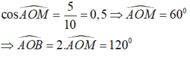
Cho đường tròn tâm O bán kính R . Tại điểm M nằm ngoài đường tròn kẻ các tiếp tuyến MA,MB với đường tròn ( A,B là các tiếp điểm ) . Vẽ đường thẳng MCD không đi qua tâm ( C nằm giữa M và D ) . OM cắt AB và (O) tại H , gọi I là trung điểm OM
a) CM 4 điểm M,A,O,B thuộc 1 đường tròn
b) CM: AB vuông góc với OM
Cho đường tròn (O,R) cố định.Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm).Gọi H là giao điểm của OM,AB
a) CM: OM vuông góc với AB và OH.OM=R2
b) Từ M kẻ cát tuyến MNP với đường tròn (O) (N nằm giữa M,P),gọi I là trung điểm NP (I khác O).Chứng minh: A,M,O,I thuộc một đường tròn và tìm tâm của đường tròn đó
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA,MB theo thứ tự C,D.Biết MA=5cm ,tính chu vi tam giác MCD
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt MA,MB lần lượt tại E,F.Xác định vị trí của điểm M để diện tích tam giác MEF nhỏ nhất
~Giải nhanh giùm mình nhé~
Cho đường tròn (O) và 1 điểm M nằm ngoài đường tròn. từ M kẻ 2 tiếp tuyến MA, MB với đường tròn(O) (A,B là 2 tiếp điểm). Gọi I là giao điểm của OM với AB
a, CM: 4 điểm M,A,O,B cùng thuộc 1 đường tròn
b, CM: OM vuông góc với AB tại I
c, Từ B kẻ đường kính BC của đường tròn (O), đường thẳng MC cắt đường tròn (O) tại D (D khác C). CM: tam giác BDC vuông, từ đó suy ra MD.MC=MI.MO
d, Qua O kẻ đường thẳng vuông góc với MC tại E và cắt đường thẳng AB tại F. CM: FC là tiếp tuyến của đường tròn (O)
....Giải giúp mình ý d nha.... mình đag cần gấp
Bài 4. (3,5 điểm) Cho điểm M nằm ngoài đường tròn (0;R) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn (0) (A, B là các tiếp điểm). Kẻ đường kính AC của đường tròn (0). Gọi H là giao điểm của AB và OM. 1) Chứng minh bốn điểm A, O, B, M cùng thuộc một đường tròn. 2) Tính tỷ số OH/OM. 3) Gọi E là giao điểm của CM và đường tròn (0). Chứng minh HE vuông góc BE.
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
b) Tính MA, AB, OK theo R.
Cho đường thẳng d và đường tròn (O;R) không có điểm chung. Kẻ OH vuộng góc với đường thẳng d tại H. Lấy điểm M bất kì thuộc d. Qua M kẻ 2 tiếp tuyến MA, MB tới đường tròn (O;R). Nối AB cắt OH,OM lần lượt tại K và I.
a, Chứng minh 5 điểm M,H,A,O,B cùng thuộc 1 đường tròn
b, Chứng minh OK.OH=OI.OM
c, Chứng minh khi M di chuyển trên d thì đường thẳng AB đi qua 1 điểm cố định
Mn giúp mình với :(
