Các câu hỏi tương tự
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:A.
π
.
r
2
h (
c
m
3
) B. (1/3)
π
.
r
2
h (
c
m...
Đọc tiếp
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
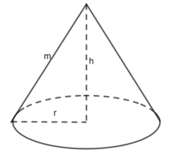
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Cho đường tròn (O; R) và điểm A sao cho OA R√2, một đường thẳng d quay quanh A cắt (O) tại M, N. Gọi I là trung điểm của MN. 1) cm OI vuông góc MN suy ra I di động trên cung tròn cố định với hai điểm giới hạn B, C thuộc (O) 2) cm A, O, B, C là bốn đỉnh của một hình vuông 3) tính theo R diện tích phần mặt phẳng giới hạn bởi AB, AC và cung nhỏ BC của đường tròn (O) 4) hãy Chỉ ra vị trí đường thẳng d khi tổng AM + AN lớn nhất và chứng minh điều đó
Đọc tiếp
Cho đường tròn (O; R) và điểm A sao cho OA = R√2, một đường thẳng d quay quanh A cắt (O) tại M, N. Gọi I là trung điểm của MN.
1) cm OI vuông góc MN suy ra I di động trên cung tròn cố định với hai điểm giới hạn B, C thuộc (O)
2) cm A, O, B, C là bốn đỉnh của một hình vuông
3) tính theo R diện tích phần mặt phẳng giới hạn bởi AB, AC và cung nhỏ BC của đường tròn (O)
4) hãy Chỉ ra vị trí đường thẳng d khi tổng AM + AN lớn nhất và chứng minh điều đó
Cho tam giác ABC có góc ACB tù, H là chân đường cao vẽ từ A . Đường tròn đường kính BH cắt AB tại điểm thứ 2 là D . Đường tròn đường kính CH cắt AC tại điểm thứ 2 là D . Đường tròn đường kính CH cắt AC tại điiểm thứ 2 là E A) CM tứ giác ADEH là tứ giác nội tiếp b) cm góc EBH EDCC) Cho BH a cân 3 , CH a, góc ABC 45. Tính diện tích hình quạt tròn giới hạn bởi cung EC và 2 bán kính đi qua E và C của đường tròn đường kính CH
Đọc tiếp
Cho tam giác ABC có góc ACB tù, H là chân đường cao vẽ từ A . Đường tròn đường kính BH cắt AB tại điểm thứ 2 là D . Đường tròn đường kính CH cắt AC tại điểm thứ 2 là D . Đường tròn đường kính CH cắt AC tại điiểm thứ 2 là E
A) CM tứ giác ADEH là tứ giác nội tiếp
b) cm góc EBH = EDC
C) Cho BH= a cân 3 , CH = a, góc ABC = 45. Tính diện tích hình quạt tròn giới hạn bởi cung EC và 2 bán kính đi qua E và C của đường tròn đường kính CH
Một cái ống rỗng dạng hình trụ hở một đầu kín một đầu (độ dày không đáng kể ) dài b (cm) và bán kính đường tròn là r (cm). Nếu người ta sơn cả bên ngoài lẫn bên trong ống thì diện tích ống được sơn bao phủ là :A.2(
π
r
2
+2
π
rb)
c
m
2
B. (
π
r...
Đọc tiếp
Một cái ống rỗng dạng hình trụ hở một đầu kín một đầu (độ dày không đáng kể ) dài b (cm) và bán kính đường tròn là r (cm). Nếu người ta sơn cả bên ngoài lẫn bên trong ống thì diện tích ống được sơn bao phủ là :
A.2( π r 2 +2 π rb) c m 2 B. ( π r 2 +2 π rb) c m 2
C. (2 π r 2 +2 π rb) c m 2 D. ( π r 2 +4 π rb) c m 2
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm AOB = 60o và bán kính đường tròn là 5,1cm (h.64).
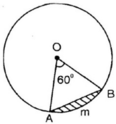
Hình 64
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm A O B = 60 o và bán kính đường tròn là 5,1cm (h.64).
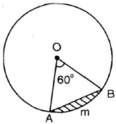
Hình 64
Từ một điểm M bên ngoài đường tròn (O,R) kẻ hai tiếp tuyến TA và TB với đường tròn đó. Biết góc AOB=120, BC=2R.
a/ Cm OT // AC
b/ Biết OT cắt đường tròn (O,R) tại Đ. Cm tứ giác AODC nội tiếp.
c/ Tính diện tích hình giới hạn bởi nửa đường tròn đường kính BC và 3 dây cung CA, DA, BD theo R.
Cho ( O ; R ),từ diểm M ngoài đường tròn ( O ) / MO 2R . Kẻ 2 tiếp tuyến MA và MB (A và B là tiếp điểm ) . Một cát tuyến bất kì qua M cắt đường tròn tại C và D ( C nằm giữa M và D ) / D cắt AB tại F , kẻ phân giác góc CAD cắt dây CD tại E và cắt đường tròn tại N . CM :a) OAMB nội tiếp b) MA MEc) Tính S hình viên phân giới hạn bởi cung nhỏ AB và dây cung AB theo R d) CM : frac{2}{CD}frac{1}{MD}+frac{1}{FD}
Đọc tiếp
Cho ( O ; R ),từ diểm M ngoài đường tròn ( O ) / MO = 2R . Kẻ 2 tiếp tuyến MA và MB (A và B là tiếp điểm ) . Một cát tuyến bất kì qua M cắt đường tròn tại C và D ( C nằm giữa M và D ) / D cắt AB tại F , kẻ phân giác góc CAD cắt dây CD tại E và cắt đường tròn tại N . CM :
a) OAMB nội tiếp
b) MA = ME
c) Tính S hình viên phân giới hạn bởi cung nhỏ AB và dây cung AB theo R
d) CM : \(\frac{2}{CD}=\frac{1}{MD}+\frac{1}{FD}\)









