Trong tam giác ACD, ta có :
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD
Suy ra : OB = (1/2).AD (tính chất đường trung bình của tam giác)
Vậy AD = 2.OB = 2.2 = 4 (cm)

Trong tam giác ACD, ta có :
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD
Suy ra : OB = (1/2).AD (tính chất đường trung bình của tam giác)
Vậy AD = 2.OB = 2.2 = 4 (cm)
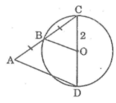
Cho đường tròn (O)bán kính =2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đg tròn và cắt đg tròn tại B và C trong đó AB=BC, Kẻ đg kính COD . Tính độ dài Ad
Cho đường tròn (O; 2 cm) và điểm A ngoài (O). Từ A kẻ cát tuyến với (O), cắt (O) tại B và C. Cho biết AB = BC và kẻ đường kính COD, tính độ dài đoạn thẳng AD
cho đường tròn O có bán kính là 2cm , cho A là một điểm nằm ngoài đường tròn sao cho OA=2R ( OA=4cm ) . kẻ tiếp tuyến AB , AC ( B và C là hai tiếp điểm ) . góc AOB = 60 . kẻ đường thẳng (d) đi qua A và cắt (O) tại 2 điểm P và Q bất kì . tính AP.AQ
Từ một điểm A nằm bên ngoài đường tròn (o), kẻ các tiếp tuyến AB,AC với đường tròn (B , C là các tiếp điểm ) a, Chứng minh tứ giác ABOC là tứ giác nội tiếp b, Cho bán kính đường tròn (O) bằng 3cm , độ dài đoạn thẳng OA bằng 5cm .Tính độ dài đoạn thẳng BC
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến AB và AC đến (O) (B,C là các tiếp điểm). Kẻ đường kính BD của đường tròn (O). Đường thẳng đi qua O vuông góc với đường thẳng AD và AD, BC lần lượt tại K, E. Gọi I là giao điểm của OA và BC.
a, C/m các tứ giác ABOC, AIKE nội tiếp đường tròn
b, C/m OI.OA=OK.OE
c, Bt OA=5cm, đường tròn (O) có bán kính R=3cm. Tính độ dài đoạn thẳng BE
cho nửa đường tròn tâm O đường kính AB bằng 2r gọi C và D là hai điểm trên nửa đường tròn sao cho C thuộc cung AD và góc COD bằng 120 độ AD cắt BC tại E AC cắt BD tại F .chứng minh rằng:
a/ 4 điểm CDEF cùng thuộc một đường tròn
b/ tính r đường tròn đi qua CDEF qua r
Cho đường tròn O bán kính R và một điểm P nằm bên ngoài đường tròn . Kẻ các tiếp tuyến PA ,PB với đường tròn ( O , R ) ( A, B là hai tiếp điểm ). Gọi C là điểm đối cứng của B qua O . Đường thẳng OC cắt đường tròn ( O ,R ) tại điểm D ( khác C) . Hai đường thẳng AD và OP cắt nhau tại Q a, Chứng minh tứ giác PAOB nội tiếp đường tròn b, Chứng mình rằng PQ mũ 2 = QA*QD c, Giả sử P cách O một khoảng 4 căn 3 cm. Tính bán kính R của đường tròn đã cho để tứ giác OAQB là hình thoi.
. Cho đường tròn ( O) và một điểm A nằm bên ngoài đường tròn O . Từ A vẽ hai tiếp AB, AC với đường tròn O ( B,C là hai tiếp điểm ) . Gọi H là giao điểm của OA và OB ..
câu A : Chứng minh OA vương góc với BC tại HCÂU b ; tỪ b KẺ đường kính BD của đường tròn O , đường thẳng AD cắt O tại E (E khácD)Chứng minh AE*AD=AH*AOCÂU C. qua O kẻ đường thẳng vương góc với đưởng thẳng AD cắt K và cắt đưởng thẳng BC tại F Chứng minh : FD là tiếp điểm của đường tròn
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn, kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ đường kính BOD. Tiếp tuyến của đường tròn tại D cắt đường thẳng BC tại E. a, Chứng minh : Tam giác ACD đồng dạng tam giác OCE b, Chứng minh : AD vuông góc với OE