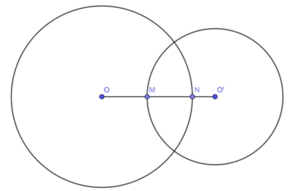
Ta có:
ON = 8cm, O'M = 6cm, OO' = 10cm
ON + O'M = OM + MN + MN + O'N = (OM + MN + O'N) + MN = OO' + MN
⇒ 8 + 6 = 10 + MN ⇒ MN = 4cm
Đáp án: D
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hai đường tròn (O; 8cm) và (O’; 6cm) có đoạn nối tâm OO’ = 11cm. Đường tròntâm O cắt OO’ tại N, đường tròn tâm O’ cắt OO’ tại M. Tính độ dài đoạn thẳng MN.
cho hai đường tròn (O;6cm) và (O'5cm) cắt nhau tại hai điểm A,B. và AB= 8cm. Khi đó độ dài đoạn nối tân OO' là :
Biết OO' > 2cm.
( kết quả làm tròn đến chữ số thập phân thứ hai ).
Câu 11. [VDC] Cho hai đường tròn (O; 10cm) và (O/; 6cm) tiếp xúc ngoài tại M. Gọi AB là tiếp tuyến chung của hai đường tròn (A (O); B (O/)). Đường thẳng AB cắt đường thẳng OO/ tại C. Độ dài O/C bằngA. 16cm. B. 24 cm. C. 28 cm. D. 34 cm. Câu 12. [VDC] Cho tam giác ABC có đường tròn nội tiếp tiếp xúc với AB, BC, CA theo thứ tự tại M, N, P; Biết BC a và chu vi tam giác ABC bằng p. Tính AM theo a và p.A. AM p + a. B. AM p -2a. ...
Đọc tiếp
Câu 11. [VDC] Cho hai đường tròn (O; 10cm) và (O/; 6cm) tiếp xúc ngoài tại M. Gọi AB là tiếp tuyến chung của hai đường tròn (A (O); B (O/)). Đường thẳng AB cắt đường thẳng OO/ tại C. Độ dài O/C bằng
A. 16cm. B. 24 cm. C. 28 cm. D. 34 cm.
Câu 12. [VDC] Cho tam giác ABC có đường tròn nội tiếp tiếp xúc với AB, BC, CA theo thứ tự tại M, N, P; Biết BC = a và chu vi tam giác ABC bằng p. Tính AM theo a và p.
A. AM = p + a. B. AM = p -2a.
C. AM = 2p – a. D. AM = – a.
Cho đường tròn tâm O' bán kính 4.5 cm; đường tròn tâm O bán kính 6cm. Hai đường tròn cắt nhau tại A và B ( O và O' thuộc 2 nửa mặt phẳng bờ là AB ). Gọi I là trung điểm của OO'. Qua A kẻ đường thẳng vuông góc với IA cắt đường tròn tâm O và đường tròn tâm O' lần lượt tại C và D
a) CM AC = AD b) Cho góc OAO' = 90 độ. Tính OO' và AB
Cho 2 đường tròn (O; 20 cm) và (O'; 15 cm) cắt nhau tại hai điểm M và N . Gọi I là giao điểm của MN và OO'
a, CM OO' vuông góc với MN
b, Cho MN = 24cm , Tính độ dài đth MI
c, Tính độ dài đoạn OO' . CM O'M là tiếp tuyến của đường tròn (O)
Cho hai đường tròn (O) và (O) có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O) và tâm O nằm trên đường tròn (O). Đường nối tâm OO cắt AB tại H, cắt đường tròn (O) tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O.a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.b) Trên cạnh AC lấy điểm D sao cho AD AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHOE, ADKO...
Đọc tiếp
Cho hai đường tròn (O) và (O') có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O') và tâm O' nằm trên đường tròn (O). Đường nối tâm OO' cắt AB tại H, cắt đường tròn (O') tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O'.
a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.
b) Trên cạnh AC lấy điểm D sao cho AD = AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHO'E, ADKO là các tứ giác nội tiếp.
c) Tứ giác AHKG là hình gì? Vì sao.
d) Tính diện tích phần chung của hình (O) và hình tròn (O') theo bán kính R.
Cho hai đường tròn ( O ) và đường tròn (O' ) tiếp xúc ngoài tại A đường nối tâm OO' cắt đường tròn ( O ) ở B , cắt đường tròn ( O') tại C . DE là 1 tiếp tuyến chung ngoài của 2 đường tròn . gọi M là giao của BD và EC
Cho đường tròn (O, 15 cm) và đường tròn (O', 20 cm) cắt nhau tại M và N. Biết MN = 24 cm. O và O' nằm khác phía so với MN
b) Tính độ dài đoạn OO'
Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm. Vẽ đường tròn (O’; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O’A cắt đường tròn (O’; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm), (O’; 3cm).