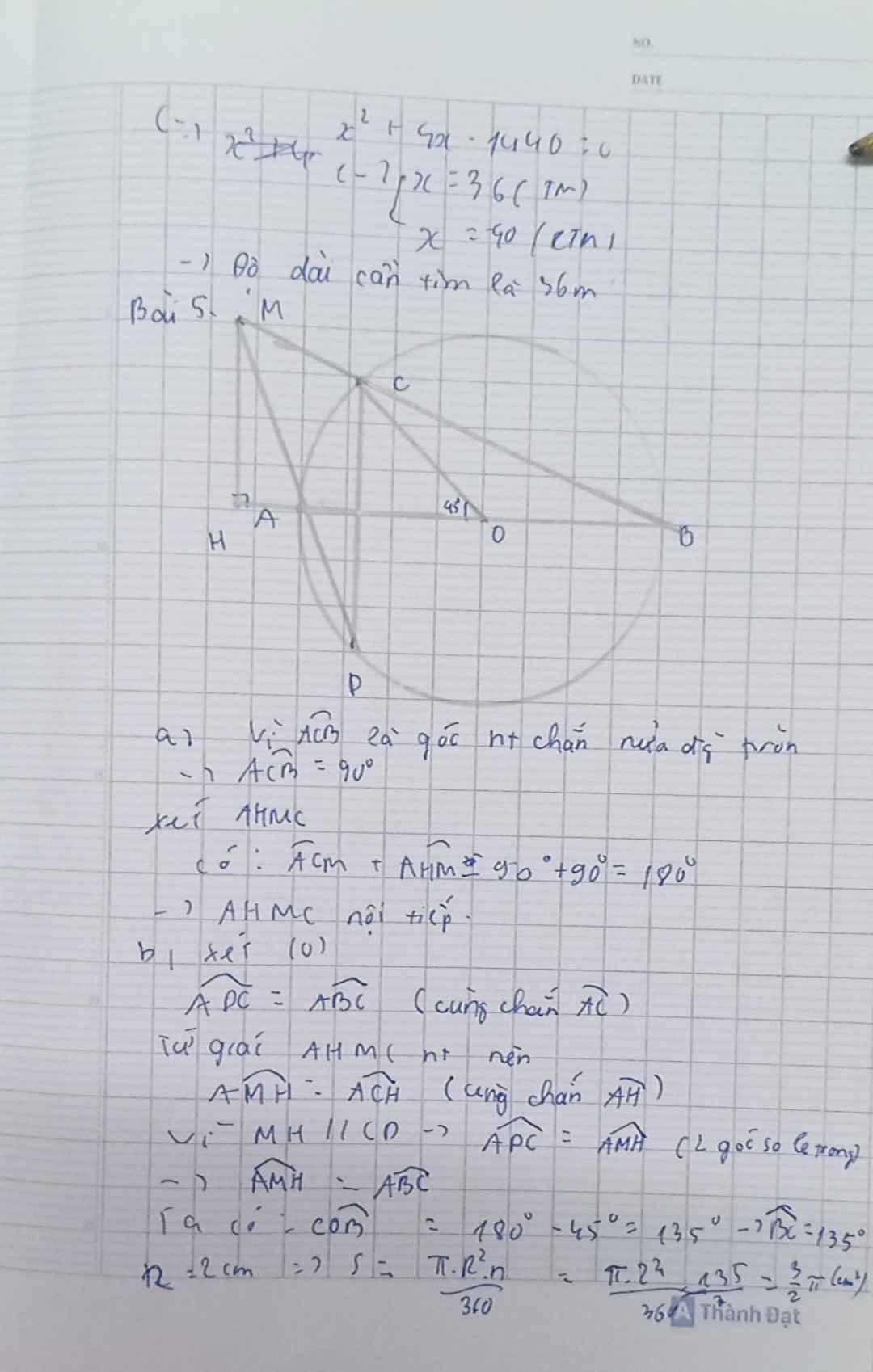
Cho đường tròn $(O ; 2 \mathrm{~cm})$ đường kính $A B$. Lấy điểm $C$ trên đường tròn sao cho $ \widehat{AO C}=45^{\circ}$. Đường thẳng qua $C$ và vuông góc với $A B$ cắt $(O)$ tại $D$. Kéo dài $B C$ và $D A$ cắt nhau tại $M$. Kẻ $M H \perp A B$ tại $H$
a) Chứng minh tứ giác $A H M C$ nội tiếp.
b) Chứng minh $\widehat{A C H}=\widehat{A B C}$
c) Tính diện tích hình quạt $O C B$
Bài làm :
a) Ta có :
\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)
\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)
Từ đó ; ta có :
\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o
\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)
a) Xét tứ giác AHMC có
góc ACM + góc AHM = 180 độ
Vậy tứ giác AHMC nội tiếp

a)có góc ACB là góc nội tiếp chắn nửa hình tròn ⇒góc ABC =90
⇒góc ACM=góc ACB =90 (2 góc kề bù)
xét tứ giác AHMC ta có
góc ACM =90
góc MHA =90 (vì MH vuông góc AB)
⇒góc ACM +MHA =180 ,lại có 2 góc này ở vị trí đối nhau
vậy tứ giác AHMC nội tiếp đường tròn
b) có góc ADC = góc ABC (góc nội tiếp cùng chăn cung AC)
có góc HMA = góc ACH (góc nội tiếp chắn cung AH)
lại có MH song song với CD ⇒góc HMA= góc ADC (2 góc so le trong)
từ đó suy ra góc ACH=góc ABC
c)có góc AOC=45⇒góc COB=180-45=135
có r=2 suy ra diện tích hình quạt OCB là S=\(\dfrac{\Pi.r^2.135}{360}\)=\(\dfrac{3}{2}\)π (cm2)
vậydiện tích hình quạt OCB =3/2π (cm2)

Vì \(\widehat{ACB}\)
a) là góc nội tiếp chắn nửa đường tròn nên \(\widehat{ACB=90}\) . Suy ra \(\widehat{ACM}=90\)
Tứ giác AHMC có \(\widehat{ACM}+\widehat{AHM}=90+90=180\) nên tứ giác AHMC nội tiếp (dpcm)
b) Trong (O), ta có: \(\widehat{ADC}=\widehat{ABC}\) ( góc nội tiếp cùng chắn cung \(\stackrel\frown{AC}\) )
Tứ giác AHMC nội tiếp nên \(\widehat{AMH}=\widehat{ACH}\) (góc nội tiếp chắn cung \(\stackrel\frown{AH}\) )
Vì MH // CD nên \(\widehat{ADC}=\widehat{AMH}\) ( 2 góc sole trong)
Từ đó suy ra, \(\widehat{AMH}=\widehat{ABC}\) (đpcm)
c) Ta có: \(\widehat{COB}=180-45=135\)
nên sđ \(\stackrel\frown{BC}\) =135
Lại có \(R=2cm\) suy ra diện tích cần tìm là \(S=\dfrac{\pi R^2n}{360}=\dfrac{\pi.2^2.135}{360}=\dfrac{3}{2}\pi\left(cm^2\right)\)
.
Câu a: Có góc ACB=90 độ(góc nt chắn nửa đt)→góc ACM=90 độ
mà góc MHA=90 độ(MH \(\perp\)AB); 2 góc ở vị trí đối nhau
⇒tứ giác AHMC nội tiếp
Câu b:
Vì AB\(\perp\)CD→ Cung AC= cung AD= 45 độ→ sđ cung DB=180- 45=135 độ
Góc DAB= 1/2 sđ cungBD=\(\dfrac{1}{2}\)135 độ= 67,5 độ
Mà góc HAM= góc DAB (đối đỉnh)= 67,5 độ
Lại có góc MCH= góc HAM (vì tứ giác AHCM nt) → góc MCH = 67,5 độ
Mà góc MCA= 90 độ (câu a)
⇒ Góc ACH= góc MCA- góc MCH= 90- 67,5= 22,5 độ
Mà góc ABC = 1/2 góc AOC (cùng chắn cung AC)= 45/2= 22,5 độ
⇒ Góc ACH = góc ABC
Câu c:
Góc COB= 180 độ- 45 độ= 135 độ
SqOCB=\(\dfrac{\pi R^2n}{360}\)=\(\dfrac{\pi.2^2.135}{360}\)= 1,5\(\pi\)(cm2)
a) Vì là góc nội tiếp chắn nửa đường tròn nên Suy ra
Tứ giác có nên tứ giác nội tiếp (đpcm).
b) Trong , ta có: (góc nội tiếp cùng chắn cung )
Tứ giác nội tiếp nên (góc nội tiếp củng chắn cung ).
Vì song song với nên ( 2 góc so le trong).
Từ đó suy ra, đpcm .
a) Xét tứ giác AHMC có
H + C = 180
mà 2 góc lại đối đỉnh
Suy ra M +H =180
Từ đây suy ra tứ giác AHMC nội tiếp đường tròn ( 2 góc đói có tổng bằng 180)
b) Có HD=HC (đường kính vuông góc với dây)
Suy ra : cung AD = CUNG AC
Mà ACH=1/2 AD
ABC=1/2 AC
Suy ra ACH = ABC
c) Squạttròn = (4x135x3.14)/360
=3/2pi
a) Có \(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn => \(\widehat{ACB}\) =\(90^o\)
\(\widehat{AMC}\) =\(90^o\) (Kề bù với \(\widehat{ACB}\)
Xét tứ giác AHMC có \(\widehat{ACM}\) +\(\widehat{AHM}\)=\(^{ }180^o\) => tứ giác AHMC nội tiếp
b) Trong (O) có \(\widehat{ADC}\) = \(\widehat{ABC}\) =\(\dfrac{1}{2}\) sđ\(\stackrel\frown{AC}\)
Có AHMC nội tiếp (câu a) => \(\widehat{AHM}\) =\(\widehat{ACH}\) =\(\dfrac{1}{2}\) sđ \(\stackrel\frown{AH}\)
VÌ MH // CD nên \(\widehat{ADC}\) =\(\widehat{AMH}\) ( 2 góc sole trong)
=> \(\widehat{AMH}\) = \(\widehat{ABC}\) ( đpcm)
a, Tứ giác AHMC nội tiếp
c, S=3/2π
a) Ta có :
Từ đó ; ta có :
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o