Đáp án A
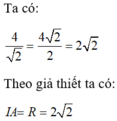
Do đó, điểm A nằm trên đường tròn đã cho. Khi đó, qua điểm A ta vẽ được đúng 1 tiếp tuyến đến đường tròn (I).
Đáp án A
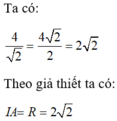
Do đó, điểm A nằm trên đường tròn đã cho. Khi đó, qua điểm A ta vẽ được đúng 1 tiếp tuyến đến đường tròn (I).
Cho đường tròn (O) và điểm A nằm bên ngoài (P). Kẻ 2 tiếp tuyến AM, AN với đường tròn (O) ( M,N là tiếp điểm). Một đường thằng d đi qua A cắt đường tròn (O) tại 2 điểm B và C ( AB<AC, d không đi qua tâm O ).
a) Cm: tứ giác AMON nội tiếp
b) Gọi I là trung điểm của BC. Đường thằng NI cắt đường tròn (O0 tại điểm thứ 2 T. Chứng minh MT//AC
c) Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở K . Cm K thuộc 1 đường thẳng cố định khi d thay đổi và thỏa mãn điều kiện đề bài
Ai giúp mình với mình đang cần gấp !! Cảm ơn
Bài 1: Cho tam giác ABC (AB < AC) nhọn nội tiếp đường tròn tâm O. Trên cạnh BC lần lượt lấy hai điểm D và E (D nằm giữa B và E) sao cho DAB = EAC. Các tia AD và AE tương ứng cắt lại đường trong (O) tại I và J.
a) Chứng minh rằng phân giác của góc BAC đi qua điểm chính giữa của cung nhỏ IJ của đường tròn (O).
b) Chứng minh rằng: Tứ giác BCJI là hình thang cân.
c) Kẻ tiếp tuyến xy của đường tròn (O) tại điểm A. Chứng minh rằng đường thẳng xy cũng là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE.
Bài 2 : Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = a^2 + b^2 + c^2 – 3ab.
Cho đường tròn (O:R). Một đường thẳng d không đi qua tâm, cắt đường tròn tại hai điểm A và B phân biệt. Trên d lấy M sao cho A nằm giữa M và B. Từ M kẻ 2 tiếp tuyến MC và MD cới đường tròn ( C và D là 2 tiếp điểm).
a) CMR: MCOD nội tiếp.
b) Gọi I là trung điểm của Ab, đường thẳng IO cắt tia MD tại K. CMR: KD.KM = KI.KO.
c) Một đường thẳng đi qua O và song song với CD, cắt các tia MC và MD lần lượt tại E và F. Xác định vị trí của M trên d sao cho diện tích tam giác MÈ đạt GTNN. Mọi người giải giúp mình câu c với, xin cảm ơn!
Cho đường tròn ( O; R ) và điểm A cố định ngoài đường tròn. Qua A kẻ 2 tiếp tuyến AM, AN với đường tròn (M và N là các tiếp điểm). Một đường thẳng d đi qua A cắt (O;R) tại B và C (AB<AC). Gọi I là trung điểm BC
a, Chứng minh A, M, N, O, I cùng thuộc 1 đường tròn
b, Chứng minh AK.AI = AB.AC
Cho đường tròn (O; R) đường kính AB và điểm C bất kỳ thuộc đường tròn (C khác A và B). Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BC ở D. Đường thẳng tiếp xúc với đường tròn tại C cắt AD ở E.
1. Chứng minh bốn điểm A, E, C, O cùng thuộc một đường tròn.
2. Chứng minh BC.BD = 4R2 và OE song song với BD.
3. Đường thẳng kẻ qua O và vuông góc với BC tại N cắt tia EC ở F. Chứng minh BF là tiếp tuyến của đường tròn (O;R).
4. Gọi H là hình chiếu của C trên AB, M là giao của AC và OE. Chứng minh rằng khi điểm C di động trên đường tròn (O; R) và thỏa mãn yêu cầu đề bài thì đường tròn ngoại tiếp tam giác HMN luôn đi qua một điểm cố định.
Cho đường tròn (O;R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thẳng d ở ngoài đường tròn (O) sao chi ID>IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
a, Chứng minh 5 điểm A, H, O, B, I cùng thuộc 1 đường tròn .
b, Giả sử AI=AO, khi đó tứ giác AOBI là hình gì ? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI .
c, Chứng minh rằng khi điểm I di chuyển trên đường thẳng d thỏa mãn: ở ngoài (O) và ID>IC thì AB luôn đi qua một điểm cố định
Cho đường tròn (O;R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thẳng d ở ngoài đường tròn (O) sao chi ID>IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
a, Chứng minh 5 điểm A, H, O, B, I cùng thuộc 1 đường tròn
b, Giả sử AI=AO, khi đó tứ giác AOBI là hình gì
c, Chứng minh rằng khi điểm I di chuyển trên đường thẳng d thỏa mãn: ở ngoài (O) và ID>IC thì AB luôn đi qua một điểm cố định
(2 điểm) Từ 1 điểm A ở ngoài đường tròn (O), kẻ tiếp tuyến AB với đường tròn (O)
( B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB, kẻ tiếp tuyến IM với đường tròn (O) ( M là tiếp điểm).
a)Chứng minh IA = IM.
b)Chứng minh Tam giác ABM là tam giác vuông tại M.
c)Vẽ đường kính BC của đường tròn (O). Chứng minh 3 điểm A, M, C thẳng hàng.
1. Cho nửa đường tròn tâm (o),, đường kính AB=6. Trên đoạn OB lấy điểm H sao cho HB=2HO. Qua H kẻ đường thẳng vuông góc với AB cắt nửa đường tròn tại điểm C. Vẽ đường tâm (I) đường kính OA cắt AC tại D. Gọi E là giao điểm của OC và BD.
a) CM AD=CD
b) CM 4 điểm O,D,C,H cùng nằm trên 1 đường tròn
c) CM BD là tiếp tuyến của đường tròn (I)
2. Cho 3 số a,b,c không âm thỏa mãn: a + b + c = 1008. CM rằng:
\(\sqrt{2016a+\frac{\left(b-c\right)^2}{2}}\) + \(\sqrt{2016b+\frac{\left(c-a\right)^2}{2}}\)+ \(\sqrt{2016c+\frac{\left(a-b\right)^2}{2}}\)\(\le\)2016\(\sqrt{2}\)
GIÚP MÌNH VỚI. PLEASE