Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
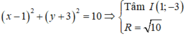
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
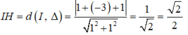
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
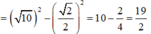
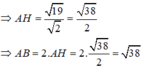
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
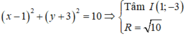
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
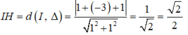
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
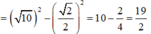
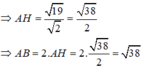
Trong mặt phẳng Oxy, cho hai điểm A(1;2) và B(-3;6)
Tìm giá trị của tham số m để đường thẳng Δ: x+y+2m+1=0 cắt đường tròn (C):(x-1)2+(y+2)2=2 tại hai điểm phân biệt A,B sao cho độ dài AB=2
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Trong hệ trục tọa đô Oxy. Cho đường tròn (C):(x-1)2+(y-2)2=5
a/Viết phương trình đường thẳng (d) đi qua gốc tọa đố và tâm của đường tròn (C)
b/Viết phương trình đường thẳng(Δ) đi qua M(1;3) cắt đường tròn (C) theo dây cung AB có độ dài bằng \(3\sqrt{2}\)
làm nhanh giúp e vs ạ
trong mặt phẳng Oxy, cho điểm I (2;-1) và đường thẳng Δ:3x+4y+3=0.Viết phương trình đường tròn tâm I cắt Δ tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB = 4
Đường tròn (C) đi qua hai điểm A(1; 2); B(3;4) và tiếp xúc với đường thẳng Δ : 3 x + y − 3 = 0 . Viết phương trình đường tròn (C), biết tâm của (C) có tọa độ là những số nguyên.
A. x 2 + y 2 − 3 x – 7 y + 12 = 0.
B. x 2 + y 2 − 6 x – 4 y + 5 = 0.
C. x 2 + y 2 − 8 x – 2 y − 10 = 0.
D. x 2 + y 2 − 2 x − 8 y + 20 = 0.
Cho đường tròn ( C) : x^2 + y^2 - 2x + 4y - 4 = 0, có tâm I và đường thẳng d : √2x + my + 1 - √2 = 0
a) Tìm m để đường thẳng cắt đường tròn (C) tại hai điểm phân biệt A, B
b) Tìm m để diện tích tam giác IAB là lớn nhất
cho đường thẳng d:x+y+2=0 và đường tròn (C): x^2+y^2-4x-2y=0. Gọi I là tâm đường tròn (C), M là điểm thuộc d. qua M kẻ tiếp tuyến MA với (C) và 1 cát tuyến cắt (C) tại B,C. Tìm tọa độ điểm M biết tam giác ABc vuông tại B và có diện tích bằng 5
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
cho đường tròn (C): \(x^2+y^2\)-8x-9=0 và điểm M(1;-1). Viết phương trình đường thẳng đi qua M và cắt (C) tại 2 điểm phân biệt A,B sao cho MA=3MB