Các câu hỏi tương tự
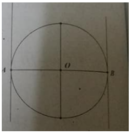
Cho đường tròn (C) có tâm O và đường kính AB. Gọi ∆ là tiếp tuyến của (C) tại điểm A. Phép tịnh tiến
T
A
B
⇀
biến ∆ thành: A. Đường kính của (C) song song với ∆. B. Tiếp tuyến của (C) tại điểm B. C. Tiếp tuyến của (C) song song với AB. D. Đường kính của (C) qua O.
Đọc tiếp
Cho đường tròn (C) có tâm O và đường kính AB. Gọi ∆ là tiếp tuyến của (C) tại điểm A. Phép tịnh tiến T A B ⇀ biến ∆ thành:
A. Đường kính của (C) song song với ∆.
B. Tiếp tuyến của (C) tại điểm B.
C. Tiếp tuyến của (C) song song với AB.
D. Đường kính của (C) qua O.
Số phát biểuđúng là:a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nób) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiếnc) Phép tịnh tiến biến tứ giác thành tứ giác bằng nód) Phép tịnh tiến biến đường tròn thành chính nóe) Phép đồng nhất biến mọi hình thành chính nóf) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kìg) Phép chiếu lên đường thẳng không là phép dời hìnhh) Với bất kì 2 điểm A, B...
Đọc tiếp
Số phát biểuđúng là:
a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
b) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiến
c) Phép tịnh tiến biến tứ giác thành tứ giác bằng nó
d) Phép tịnh tiến biến đường tròn thành chính nó
e) Phép đồng nhất biến mọi hình thành chính nó
f) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kì
g) Phép chiếu lên đường thẳng không là phép dời hình
h) Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có A’B = AB’.
i) Nếu phép dời hình F biến tam giác ABC thành tam giác A’B’C’ thì trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’.
k) Phép tịnh tiến theo vectơ là phép đồng nhất.
l) Nếu phép dời hình biến điểm A thành điểm B ( B ≠ A ) thì nó cũng biến điểm B thành A
m) Nếu phép dời hình biến điểm A thành điểm B và biến điểm B thành điểm C thì AB = BC
A.5
B.6
C.7
D.8
cho hàm số y=x^3-3x^3+2(C). viết pt tiếp tuyến của (C) a) Tại điểm có tung độ bằng 2 b) Tại điểm M mà tiếp tuyến tại M song song với đường thẳng y=6x+1
Cho đường tròn tâm O và hai tiếp tuyến song song với nhau tiếp xúc với đường tròn tại hai điểm A và B.Mệnh đề nào sau đây đúng? A
O
A
→
-
O
B
→
B
A
B
→
-...
Đọc tiếp
Cho đường tròn tâm O và hai tiếp tuyến song song với nhau tiếp xúc với đường tròn tại hai điểm A và B.Mệnh đề nào sau đây đúng?
A O A → = - O B →
B A B → = - O B →
C OA = - OB
D AB = - BA
Cho hình thang ABCD có AB // CD và AB 2a, BC CD DA a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.b) Gọi O là trung điểm của AB, O là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO ⊥ (SBC).c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.d) Tìm một điểm cách đ...
Đọc tiếp
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
x
-
2
2
+
y
+
1
2
9
Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k
-
1
3...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x - 2 2 + y + 1 2 = 9 Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k= - 1 3 và phép tịnh tiến theo vecto v → = ( 1 ; - 3 ) . Tìm bán kính R’ của đường tròn (C’).
A. 9
B. 3
C. 27
D. 1
cho hàm số y=f(x)=-x3+2x2-x+5 có đồ thị (C). Tìm tham số m để tiếp tuyến Δ của đồ thị (C) tại tiếp điểm A(2;3) song song với đường thẳng (d): (m2-3m-5)x-y-2m+19=0
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Cho hàm số y = x3 – 3x2 + 1 (C). Tìm tổng hoành độ của hai điểm A; B trên đồ thị hàm số sao cho tiếp tuyến của đồ thị (C) tại A; B song song với nhau và A B = 4 2
A: 1
B: 2
C: 3
D: 5