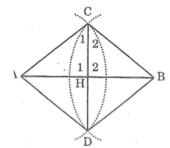
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD = ΔBCD(c.c.c)
Suy ra: ∠C1 = ∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C1 = ∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC = ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 = ∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 = ∠H2 = 90o ⇒ CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB









