Các câu hỏi tương tự
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường thẳng vuông góc với OC tại O cắt tia By ở D. C/m CD=AC+BD
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng 1 nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường thẳng vuông góc với OC tại O cắt tia By ở D. C/m CD=AC+BD
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng CD = AC + BD.
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng CD = AC + BD.
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng CD = AC + BD.
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC cắt By tại D. CMR CD = AC + BD
Gọi O là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax và By vuông góc với AB. Trên tia Ax lấy điểm C bất kì , đường vuông góc với OC tại O cắt tia By ở D. C/minh: CD = AC + BD
Cho đoạn thẳng AB, O là trung điểm của AB, trên cùng 1 nửa mặt phẳng bờ AB vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng: CD=AC+BD
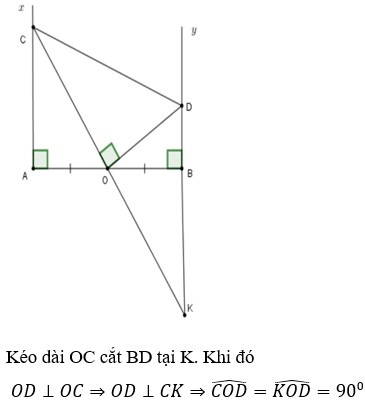
Cho đoạn thẳng AB, gọi O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm bất kỳ thuộc tia Ax ( C khác A ), đường thẳng vuông góc với OC tại O cắt By ở D. Tia CO cắt đường thẳng BD ở K. Chứng minh:
a) AC//BD
b) \(\Delta AOC=\Delta BOK\), từ đó suy ra AC = BK.
c) CD = AC + BD
2/ Cho đoạn thẳng AB, gọi O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm bất kì thuộc tia Ax (C khác A), đường thẳng vuông góc với OC tại O cắt By ở D. Tia CO cắt đường thẳng BD ở K.
a/ Chứng minh tam giác AOC = tam giác BOK, từ đó suy ra AC = BK và OC = OK.
b/ Chứng minh CD = AC + BD.