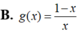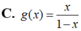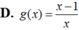Các câu hỏi tương tự
Cho hai hàm số
f
(
x
)
l
o
g
2
x
,
g
(
x
)
2
x
. Xét các mệnh đề sau: I. Đồ thị hai hàm số đối xứng với nhau qua đường thẳng y x II. Tập xác định của hai hàm số trên là R III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm IV. Hai hàm số đều đồng biến trên tập xác định của nó Có bao nhiêu mệnh đề đún...
Đọc tiếp
Cho hai hàm số f ( x ) = l o g 2 x , g ( x ) = 2 x . Xét các mệnh đề sau:
I. Đồ thị hai hàm số đối xứng với nhau qua đường thẳng y = x
II. Tập xác định của hai hàm số trên là R
III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm
IV. Hai hàm số đều đồng biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Gọi (C) là đồ thị của hàm số
y
lo
2018
x
và
C
là đồ thị của hàm số y f(x) ,
C
đối xứng với (C) qua trục tung. Hàm số
y
f
x
đồng biến trên khoảng nào sau đây?
Đọc tiếp
Gọi (C) là đồ thị của hàm số y = lo 2018 x và C ' là đồ thị của hàm số y = f(x) , C ' đối xứng với (C) qua trục tung. Hàm số y = f x đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
;
(
0
a
≠
1
)
qua điểm I(2;1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ; ( 0 < a ≠ 1 ) qua điểm I(2;1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Đồ thị hàm số y f(x) đối xứng với đồ thị của hàm số
y
a
x
(
a
0
,
a
≠
1
)
qua điểm I(1;1). Giá trị của biểu thức
2
+
log
a
1
2018
bằng
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = a x ( a > 0 , a ≠ 1 ) qua điểm I(1;1). Giá trị của biểu thức 2 + log a 1 2018 bằng
![]()
![]()
![]()
![]()
Đồ thị hàm số
y
f
(
x
)
đối xứng với đồ thị hàm số
y
log
a
x
;
(
0
a
≠
1
)
qua điểm
I
2
;
1
. Giá trị của biểu thức
f
4
-
a...
Đọc tiếp
Đồ thị hàm số y = f ( x ) đối xứng với đồ thị hàm số y = log a x ; ( 0 < a ≠ 1 ) qua điểm I 2 ; 1 . Giá trị của biểu thức f 4 - a 2019 bằng
A. 2023
B. -2023
C. 2017
D. -2017
Cho hàm số
y
x
-
1
x
+
m
,
m
≠
-
1
, có đồ thị (C). Tìm m để...
Đọc tiếp
Cho hàm số y = x - 1 x + m , m ≠ - 1 , có đồ thị (C). Tìm m để đồ thị (C) nhận I (2;) làm tâm đối xứng.
A. m = 1 2
B. m = - 1 2
C. m = 2
D. m = -2
Cho hàm số y = m + 1 x - 2 m + 1 x - 1 (m là tham số) có đồ thị (G).
Xác định m để đồ thị (G) đi qua điểm (0; -1).
Cho hàm số
y
x
x
-
1
có đồ thị (C) .Gọi
∆
là tiếp tuyến tại điểm M(x0; y0) (với x0 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất? A.
7
π
2
B.
3
π...
Đọc tiếp
Cho hàm số y = x x - 1 có đồ thị (C) .Gọi ∆ là tiếp tuyến tại điểm M(x0; y0) (với x0 > 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất?
A. 7 π 2
B. 3 π 2
C. 5 π 2
D. π 2